Cho hình chóp S.ABC có SA=1, SB=2, SC=3 và A S B ^ = 60 o , B S C ^ = 120 o , C S A ^ = 90 o . Tính thể tích khối chóp S.ABC
A. 2 2
B. 2
C. 1/6
D. 1/3
Cho hình chóp tam giác S.ABC có A S B ^ = B S C ^ = C S A ^ = 60 ° và S A = 1 , S B = 2 , S C = 3 . Thể tích của hình chóp S.ABC bằng
A. 2 6
B. 2 3
C. 2 2
D. 2 12
Cho hình chóp S.ABC có SA = 1, SB = 2, SC = 3 và A S B ^ = 60 ° , B S C ^ = 120 ° , C S A ^ = 90 ° . Tính thể tích khối chóp S.ABC.
A. 2 2
B. 2
C. 2 6
Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM, 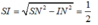
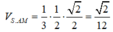
Ta có 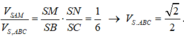
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a; SB=a 2 , SC=a 3 . Tính khoảng cách từ S đến mặt phẳng (ABC).
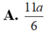
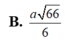
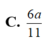
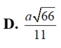
Cho hình chóp S.ABC có ASB = BSC = CSA = 60 ° ,SA = 2,SB = 3. SC = 6 Tính thể tích khối chóp S.ABC
A. 6 2 ( đ v t t )
B. 18 2 ( đ v t t )
C. 9 2 ( đ v t t )
D. 3 2 ( đ v t t )
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc với nhau và S A = 2 3 ; S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC.
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Đáp án C
Thể tích khối chóp S.ABC là
V = 1 6 S A . S B . S C = 1 6 .2 3 .2.3 = 2 3
Cho hình chóp S.ABC có SA;SB;SC đôi một vuông góc với nhau và S A = 2 3 , S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC
A. V = 12 3
B. V = 4 3
C. V = 2 3
D. V = 6 3
Đáp án C
Thể tích khối chóp là V = 1 6 .2 3 .2.3 = 2 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và S A = 2 3 , SB=2; SC=3. Tính thể tích khối chóp S.ABC
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng:
A. 300
B. 900
C. 600
D. 450
Hình chóp S.ABC có SA = SB = SC = a, \(\widehat{ASB}=90^o,\widehat{BSC}=60^o,\widehat{ASC}=120^o\). Tính góc giữa đt SC và (SAB)
\(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\)
\(AC=\sqrt{SA^2+SC^2-2SA.SC.cos120^0}=\sqrt{3}\)
\(BC=\sqrt{SB^2+SC^2-2SB.SC.cos60^0}=a\)
\(\Rightarrow AB^2+BC^2=AC^2\Rightarrow\Delta ABC\) vuông tại B
Gọi H là hình chiếu vuông góc của S lên (ABC) \(\Rightarrow\) H là tâm đường tròn ngoại tiếp ABC (do SA=SB=SC)
\(\Rightarrow\) H trùng trung điểm AC
Gọi M là trung điểm SA \(\Rightarrow MH||SC\Rightarrow\) góc giữa SC và (SAB) bằng góc giữa MH và (SAB)
Gọi N là trung điểm AB \(\Rightarrow HN\perp AB\Rightarrow AB\perp\left(SHN\right)\)
Trong mp (SHN), kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\)
\(\Rightarrow\widehat{KMH}\) là góc giữa SC và (SAB)
\(SH=\sqrt{SA^2-\left(\dfrac{AC}{2}\right)^2}=...\)
\(MH=\dfrac{1}{2}SA=...\) (trung tuyến ứng với cạnh huyền)
\(NH=\dfrac{1}{2}BC=...\) (đường trung bình)
\(\Rightarrow\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}\Rightarrow HK=...\)
\(\Rightarrow sin\widehat{KMH}=\dfrac{HK}{MH}=...\)
Cho hình chóp S.ABC có SA = SB = SC = a. ASB = 60 ∘ , BSC = 90 ∘ , CSA = 120 ∘ . Tính thể tích hình chóp S.ABC
A. 2 a 3 6
B. 2 a 3 12
C. 2 a 3 3
D. 2 a 3 4