Cho bốn điểm bất kì A; B; C; D. Mệnh đề nào sau đây đúng?
A ![]()
B ![]()
C ![]()
D ![]()
Cho bốn điểm bất kì A; B; C; D. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
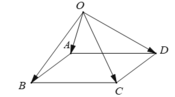
Trong không gian cho điểm O bất kì và bốn điểm A, B, C, D không thẳng hàng. Chứng minh điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: O A → + O C → = O B → + O D →
+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: 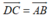 .
.
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
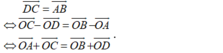
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
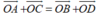
cho điểm phân biệt A ,B ,C ,D ,E không thẳng hàng nhưng bốn điểm A ,B, C, D thẳng hàng .
a) Hãy kể tên các đoạn thẳng có đầu mút là hai trong năm điểm đã cho.?
b) Có bao nhiêu đường thẳng đi qua hai điểm bất kì trong số năm điểm đã cho?
a: Có \(C^2_5\left(đoạn\right)\)
b: Có 5 đường thẳng đi qua hai điểm bất kì
Cho bốn số nguyên dương khác nhau thỏa mãn tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì luôn chia hết cho 3. Tính giá trị nhỏ nhất của tổng bốn số này
Gọi 4 số cần tìm là a, b, c, d
với 0<a<b<c<d
Vì tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3 nên các số a, b, c, d khi chia cho 2 hoặc 3 đều phải có cùng số dư
Để a+b+c+d có giá trị nhỏ nhất thì a, b, c, d phải nhỏ nhất và chia 2 hoặc 3 dư 1
Suy ra: a=1
b=7
c=13
d=19
Vậy giá trị nhỏ nhất của tổng 4 số này là: 1+7+13+19=40
Gọi 4 số cần tìm là a, b, c, d (a, b, c, d thuộc n*)
với 0<a<b<c<d
Vì tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3 nên các số a, b, c, d khi chia cho 2 hoặc 3 đều phải có cùng số dư
Để a+b+c+d có giá trị nhỏ nhất thì a, b, c, d phải nhỏ nhất và chia 2 hoặc 3 dư 1
Suy ra: a=1
b=7
c=13
d=19
Vậy giá trị nhỏ nhất của tổng 4 số này là: 1+7+13+19=40
Nếu cảm thấy đúng thì k cho mình cái!
Cho bốn số nguyên dương khác nhau thỏa mãn tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3. Tính giá trị nhỏ nhất của tổng bốn số này ?
Cho bốn số nguyên dương khác nhau thỏa mãn tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3. Tính giá trị nhỏ nhất của tổng bốn số này
cho bốn điểm A, B, C, D bất kì. Chứng minh rằng : \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)
Giúp mk vs, mk hứa tick cho 4 cái
cho bốn số nguyên dương khác nhau thỏa mãn tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3 . tính giá trị nhỏ nhất của tổng bốn số này
Gọi 4 số cần tìm là a, b, c, d
với 0<a<b<c<d
Vì tổng của hai số bất kì chia hết cho 2 và tổng của ba số bất kì chia hết cho 3 nên các số a, b, c, d khi chia cho 2 hoặc 3 đều phải có cùng số dư
Để a+b+c+d có giá trị nhỏ nhất thì a, b, c, d phải nhỏ nhất và chia 2 hoặc 3 dư 1
Suy ra: a=1
b=7
c=13
d=19
Vậy giá trị nhỏ nhất của tổng 4 số này là: 1+7+13+19=40
Cho đường tròn (O;R)), đường kính AB. Gọi I là điểm chính giữa cung AB. Lẫy điểm M bất kì trên đoạn thẳng OA (M khác OO và A)A). Tia IM cắt đường tròn tại điểm thứ hai N. Đường thẳng qua M, vuông góc với AB cắt đoạn thẳng BN tại C. a) Chứng minh bốn điểm A, M,C,N cùng thuộc một đường tròn. b) Tính số đo góc AMN và chứng minh AM=MC. c) Khi M thay đổi trên đoạn OA, chứng minh MN<R.
a) dễ thấy \(\widehat{AMC}\) \(=\) \(90^o\) xét (O) có đường kính \(AB\) \(\Rightarrow\) \(\widehat{ANB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\) \(\widehat{ANB}\) \(=90^o\) hay \(\widehat{ANC}\) \(=90^o\) . tứ giác \(ANCM\) có :
\(\widehat{AMC}\) \(+\) \(\widehat{ANC}\) \(=90^o+90^o=180^o\) \(\Rightarrow\) tứ giác \(ANCM\) nội tiếp 4 điểm \(A,N,C,M\) cùng \(\in\) 1 đường tròn
b) vì \(AB\) là đường kính của (O) \(\Rightarrow\) \(\stackrel\frown{AB}\) \(=180^o\)
mà \(I\) là điểm chính giữa của \(\stackrel\frown{AB}\)
\(\Rightarrow\) \(A=\dfrac{\stackrel\frown{AB}}{2}\) \(=\dfrac{180^o}{2}=90^o\)
có \(\widehat{ANI}\) là góc nội tiếp chắn \(\stackrel\frown{IA}\)
\(\Rightarrow\) \(\widehat{ANI}\) \(=\dfrac{1}{2}\) ; \(A=\dfrac{1}{2}.90^o\) \(=45^o\) hay \(\widehat{ANM}\) \(=45^o\) . mặt khác , tứ giác \(ANCM\) nội tiếp \(\Rightarrow\) \(\widehat{ANM}\) \(=\) \(\widehat{ACM}\) mà \(\widehat{ANM}\) \(=45^o\) \(\Leftrightarrow\) \(\widehat{ACM}\) \(=45^o\) lại có \(\Delta ACM\) cuông tại \(M\) \(\Rightarrow\) \(\Delta ACM\) vuông cân tại \(M\)
\(\Rightarrow\) \(AM=CM\)
c) kẻ đường kính \(ID\) của (O) :
có : \(MN=IN-IM\) mà \(IN\) là dây của (O) nên hiển nhiên \(IN\le ID\) nhưng do \(IN\) không qua (O) nên \(IN< ID\) (1) , dễ dàng chứng minh \(IO\perp AB\) tại \(O\)
do vậy : \(\Delta IOM\) vuông tại (O) \(\Rightarrow\) \(IM>IO\) ( không xảy ra dấu " = " vì \(M\) không trùng với \(O\) )
\(\Leftrightarrow\) \(-IM< -IO\) (2)
từ (1) và (2)
\(\Rightarrow\) \(IN-IM< ID-IO\) \(\Leftrightarrow\) \(MN< OD\) \(=R\)
vậy ta có \(đpcm\)