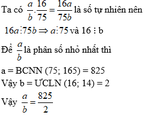c) Tìm phân số tối giản a b nhỏ nhất a , b ∈ N * để khi nhân a b với phân số 16 75 hoặc 14 165 đều được mỗi tích là số tự nhiên

Những câu hỏi liên quan
Tìm n thuộc N để phân số:
A = (4n+5)/(3n+2)
a, tối giản
b, rút gọn được
c, đạt giá trị lớn nhất, nhỏ nhất
Cho phân số A=n - 5 trên n + 1
a. Tìm n để A có giá trị là số nguyên âm
b. Tìm n để A có giá trị nhỏ nhất, lớn nhất
c. Tìm n để A là phân số tối giản
Giúp mình vơis mình cần cách làm luôn nhé
Xem chi tiết
A.
B
C
Nhé chứ ko liền nhau
Cho phân số B=4n+1/2n-3,n thuộc z
a, Tìm n để B là phân số tối giản
b, Tìm n để B đạt giá trị nhỏ nhất, giá trị lớn nhất và tính giá trị đó
Xem chi tiết
ban hoc lop may vay
Tìm phân số tối giản a/b nhỏ nhất (a, b thuộc N*) để khi a/b nhân với các phân số 14/75, 21/100 được mỗi tích là số tự nhiên
tìm phân số tối giản a/b nhỏ nhất (a,b ϵ N*) để khi nhân a/b với các phân số 15/32; 25/24 đc mỗi tích là số tự nhiên.
Ta có \(\frac{a}{b}\)*\(\frac{15}{32}\)=\(\frac{15a}{32b}\)
Mà ƯCLN(15;32)=1=>a\(⋮\)32;15\(⋮\)b(1)
\(\frac{a}{b}\)*\(\frac{25}{24}\)=\(\frac{25a}{24b}\)
Mà ƯCLN(24;25)=1=>a\(⋮\)24;25\(⋮\)b(2)
Từ (1) và (2)=>aEBC(24;32);bEƯC(25;15)
Mà \(\frac{a}{b}\) là phân số nhỏ nhất
=>aEBCNN(24;32);bEƯCLN(25;15)
=>a=96;b=5
Vậy phân số cần tìm là:\(\frac{96}{5}\)
Đúng 0
Bình luận (0)
tìm phân số tối giản a/b nhỏ nhất(a,b thuộc N*) để khi nhân a/b với phân số 16/75 hoặc 14/165 thì các tích đều là sô tự nhiên?
a)Tìm nϵ N* để 2n+1/ n(n+1) là phân số tối giản
b) Giá trị nhỏ nhất của n là bao nhiêu
a) Để phân số 2n+1/ n(n+1) là phân số tối giản thì tử và mẫu phải là các số nguyên tố cùng nhau.
Ta có thể phân tích 2n+1 thành (2n+1) = 2n + 1
Vậy phân số trên có thể đưa về dạng:
2n + 1
n(n+1)
ƯCLN(n, n+1) = 1 vì n và n+1 là 2 số liên tiếp.
Do đó, n(n+1) là số nguyên tố cùng nhau với 2n+1 khi và chỉ khi 2n+1 không chia hết cho n và n+1.
Điều này có nghĩa là 2n+1 phải là số lẻ (vì n và n+1 luôn có một số chẵn).
b) Giá trị nhỏ nhất của n để phân số trên là phân số tối giản sẽ xảy ra khi 2n+1 và n(n+1) là 2 số nguyên tố cùng nhau và 2n+1 là số lẻ nhỏ nhất.
Vậy để 2n+1 là số lẻ nhỏ nhất, n phải là số chẵn nhỏ nhất.
Do đó, ta lần lượt thử giá trị của n và tìm số lẻ nhỏ nhất làm cho phân số trên là phân số tối giản:
Khi n = 2:
2n + 1 = 5 và n(n+1) = 6
GCD(5,6) = 1.
Vậy n = 2 làm cho phân số trên là phân số tối giản.
Vậy giá trị nhỏ nhất của n là 2.
Đúng 2
Bình luận (0)
Tìm phân số tối giản a/b nhỏ nhất (a ,b thuộc N* ) Để khi nhân với các phân số 55/16;25/24 được một tích là số tự nhiên
Tìm phân số tối giản a b nhỏ nhất (a,b ∈ N*) để khi nhân a b với phân số 16 75 hoặc 14 165 đều được mỗi tích là số tự nhiên.