Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng CD ⊥ CA và CD ⊥ (SCA).

Những câu hỏi liên quan
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng \(CD\perp CA,CD\perp\left(SCA\right)\) ?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC a, cạnh bên SA vuông góc với đáy, SA a
3
. Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB). A.
3
2
B. 1 C.
21
7
D.
2
7
7
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, SA = a 3 . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB).
A. 3 2
B. 1
C. 21 7
D. 2 7 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC a, cạnh bên SA vuông góc với đáy,
S
A
a
3
. Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB) A.
3
2
B. 1 C.
21
7
D. 2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, S A = a 3 . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB)
A. 3 2
B. 1
C. 21 7
D. 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại
B
,
B
C
a
, cạnh bên SA vuông góc với đáy,
S
A
a
3
. Gọi M là trung điểm của AC. Tính côtang góc giữa hai mặt phẳng (SBM) và (SAB). A.
3
2
B. 1 C.
21
7
D.
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , B C = a , cạnh bên SA vuông góc với đáy, S A = a 3 . Gọi M là trung điểm của AC. Tính côtang góc giữa hai mặt phẳng (SBM) và (SAB).
A. 3 2
B. 1
C. 21 7
D. 2 7 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A,AB=a√3 , cạnh bên SA vuông góc với mặt đáy , SA = a√3/2 , M là trung điểm của BC. a. Chứng minh BC vuông góc với (SAM) B. Tính góc giữa đường thẳng SM và mặt phẳng (ABC)
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ
Đúng 1
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,BCa, cạnh bên SA vuông góc với đáy ,SAasqrt[]{3} .Gọi M là trung điểm của AC.Tính cot góc giữa hai mặt phẳng left(SBMright) và left(SABright).
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\),\(BC=a\), cạnh bên \(SA\) vuông góc với đáy ,\(SA=a\sqrt[]{3}\) .Gọi \(M\) là trung điểm của \(AC\).Tính cot góc giữa hai mặt phẳng \(\left(SBM\right)\) và \(\left(SAB\right)\).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA 2a. Gọi M là trung điểm của SC. Tính côsin của góc
α
là góc giữa đường thẳng BM và mặt phẳng (ABC). A. cos
α
7
14
B. cos
α
2
7
7
C. cos
α
...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA = 2a. Gọi M là trung điểm của SC. Tính côsin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
A. cos α = 7 14
B. cos α = 2 7 7
C. cos α = 5 7
D. cos α = 2 7
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA2a. Gọi M là trung điểm của SC. Tính côsin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC). A.
cos
α
7
14
B.
cos
α
2
7
7
C.
cos
α
5...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA=2a. Gọi M là trung điểm của SC. Tính côsin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
A. cos α = 7 14
B. cos α = 2 7 7
C. cos α = 5 7
D. cos α = 21 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
B
;
A
B
3
a
;
B
C
4
a
. Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo giữa SC và mặt phẳng đáy bằng
60
°
. Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng A.
a
3
B. ...
Đọc tiếp
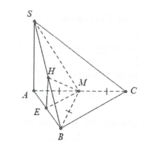
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B ; A B = 3 a ; B C = 4 a . Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo giữa SC và mặt phẳng đáy bằng 60 ° . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. a 3
B. 10 a 3 79
C. 5 a 3
D. 5 a 2
Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
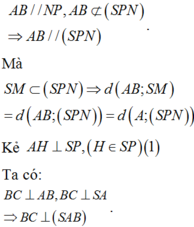
Mà
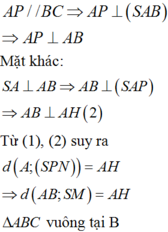
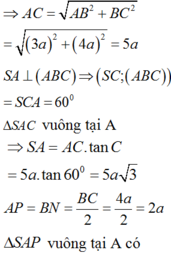
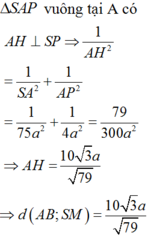
Chọn: B
Đúng 0
Bình luận (0)