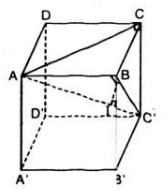
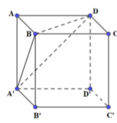
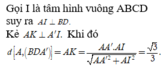Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D tới đường chéo AC' bằng nhau. Tính khoảng cách đó.

Những câu hỏi liên quan
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ các điểm B, C, D, A', B' và D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó.
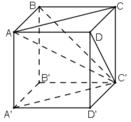
a) Ta có: ∆ ABC’ = ∆ C’CA = ∆ADC’=∆ AA’C’ =∆ C’B’A = ∆C’D’A (c.c.c)
⇒ Các đường cao hạ từ B; C; D; A’; B’; D’ xuống AC’ bằng nhau
( chú ý: các tam giác trên đều có chung cạnh AC’)
Gọi khoảng cách đó là h.
Ta có: CC’ = a; 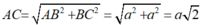
ΔC’AC vuông tại C, có hai cạnh góc vuông là CA và CC’. Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
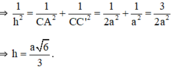
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D' tới đường chéo AC' bằng nhau. Tính khoảng cách đó ?
Điểm A cách đều ba đỉnh, của tam giác đều A'BD vì ta có AB = AD = AA' = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có :
\(C'B=C'D=C'A'=a\sqrt{2}\)

Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng các khoảng cách từ điểm B, C, D, A', B', D' đến đường chéo AC' đều bằng nhau. Tính khoảng cách đó ?
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Khoảng cách từ điểm D đến mặt phẳng ((ADB) bằng A. a B.
a
2
2
C.
a
3
3
D.
a
6...
Đọc tiếp
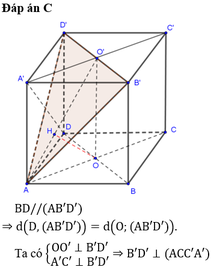
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ điểm D đến mặt phẳng ((AD'B') bằng
A. a
B. a 2 2
C. a 3 3
D. a 6 3
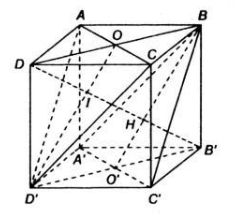
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 . Tính khoảng cách d từ điểm A đến mp (BDA')
Giải chi tiết:

Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có :
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Tính khoảng cách từ điểm A đến
(
A
’
B
D
)
theo a. A.
2
a
3
.
B.
a
3
3
.
C.
a
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Tính khoảng cách từ điểm A đến ( A ’ B D ) theo a.
A. 2 a 3 .
B. a 3 3 .
C. a 3 .
D. a 3 6 .
Phương pháp:
Cho tứ diện vuông ABCD (vuông tại đỉnh A), AH là đường vuông góc ứng với mặt huyền, khi đó:
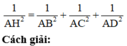

Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (ABC) theo a. A.
a
2
2
B.
a
3
3
C.
a
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC) theo a.
A. a 2 2
B. a 3 3
C. a 3 2
D. a 2 3
Đáp án A
Ta có: 1 d 2 = 1 A B 2 + 1 A A ' 2 = 2 a 2 ⇒ d = a 2 2 .
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh a
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng (BDA) bằng A.
3
B.
2
2
C.
3
3
D.
6
4
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng (BDA') bằng
A. 3
B. 2 2
C. 3 3
D. 6 4