Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình: x − 3 2 + y + 1 2 = 9 .
Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1; 2) tỉ số k = -2
Trong mặt phẳng tọa độ Oxy, cho đường tròn C có phương trình : x^2 + y^2 - 12x - 4y + 36 = 0. Viết phương trình đường tròn C1 tiếp xúc với hai trục tọa độ Ox, Oy đồng thời tiếp xúc với C.
Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : x - 2 2 + y - 3 2 = 32 thành đường tròn (C’) có phương trình:
A. x - 3 / 2 2 + y 2 = 16
B. x - 3 / 2 2 + y - 2 2 = 8
C. x - 3 2 + y - 2 2 = 32
D. x - 3 / 2 2 + y 2 = 8
Phép vị tự tâm H (1; -3) tỉ số k = 1/2, biến tâm I(2; 3) của (C) thành I’(x; y)
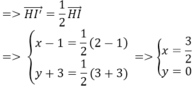
biến bán kính R = 4√2 thành R' = 2√2 ⇒ phương trình (C’) là:
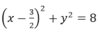
Đáp án D
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x - 1 2 + y - 1 2 = 4 Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k=2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x - 1 2 + y - 2 2 = 8
B. x - 2 2 + y - 2 2 = 8
C. x + 2 2 + y + 2 2 = 16
D. x - 1 2 + y - 2 2 = 16
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x − 1 2 + y − 1 2 = 4. Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x − 1 2 + y − 1 2 = 8.
B. x − 2 2 + y − 2 2 = 8.
C. x + 2 2 + y + 2 2 = 16.
D. x − 2 2 + y − 2 2 = 16.
Đáp án D
(C) có tâm I(1;1)và bán kính R = 2
Giả sử V 2 O : C → C ' , trong đó (C')có tâm I ' a ; b , bán kính R'
Ta có: a = 2.1 = 2 b = 2.1 = 2 ⇒ I ' 2 ; 2 và R ' = 2.2 = 4 ⇒ C ' : x − 2 2 + y − 2 2 = 16
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): ( x + 1 ) 2 + ( y - 3 ) 2 = 4 . Phép tịnh tiến theo vectơ v → = 3 ; 2 biến đường tròn (C) thành đường tròn có phương trình nào dưới đây
A. ( x + 2 ) 2 + ( y + 5 ) 2 = 4
B. ( x - 1 ) 2 + ( y + 3 ) 2 = 4
C. ( x + 4 ) 2 + ( y - 1 ) 2 = 4
D. ( x - 2 ) 2 + ( y - 5 ) 2 = 4
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x - 3 2 + y - 1 2 = 4 . Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:
A. x 2 + y 2 - 6 x - 2 y - 6 = 0
B. x 2 + y 2 - 2 x - 6 y + 6 = 0
C. x 2 + y 2 + 6 x - 2 y - 6 = 0
D. x 2 + y 2 + 6 x + 2 y + 6 = 0
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x - 2 2 + y + 4 2 = 9 và đường tròn (C’) có phương trình x - 3 2 + y + 3 2 = 9 . Phép đối xứng tâm K biến (C) thành (C’). tọa độ của K là:
A. K(2; -4)
B. K(3; -3)
C. K(-7/2;5/2)
D. K(5/2; -7/2)
Đường tròn (C) có tâm I(2; -4), bán kính R= 3
Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3
Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).
Khi đó; tâm đối xứng K là trung điểm IJ.
x K = 2 + 3 2 = 5 2 y K = ( − 4 ) + ( − 3 ) 2 = − 7 2
⇒ K 5 2 ; - 7 2
Đáp án D
Trong mặt phẳng tọa độ Oxy cho đường (C) có phương trình x 2 + y 2 - 4 x + 6 y - 3 = 0 . Qua phép vị tự tâm H(1;3) tỉ số k = -2, đường tròn (C) biến thành đường tròn (C’) có phương trình.
A. x 2 + y 2 + 2 x − 30 y + 160 = 0
B. x 2 + y 2 − 2 x − 30 y + 162 = 0
C. x 2 + y 2 + 2 x − 30 y + 162 = 0
D. x 2 + y 2 − 2 x − 30 y + 160 = 0
( C ) ⇒ ( x − 2 ) 2 + ( y + 3 ) 2 = 16 tâm I(2;-3); bán kính R=4
V H ; − 2 I = I ' x ; y ⇔ H I ' → = − 2 H I →
I’(-1; 15)
R’= |k|R = |-2| . 4 = 8
Vậy phương trình đường tròn (C) là: x + 1 2 + y − 15 2 = 64
Hay x 2 + y 2 + 2 x − 30 y + 162 = 0
Đáp án C
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C) x + 1 2 + ( y - 3 ) 2 = 4 qua phép tịnh tiến theo vectơ v → =(3;2) là đường tròn có phương trình:
A. x + 2 2 + ( y + 5 ) 2 = 4
B. x - 2 2 + ( y - 5 ) 2 = 4
C. x - 1 2 + ( y + 3 ) 2 = 4
D. x + 4 2 + ( y - 1 ) 2 = 4