Chứng minh nhận xét 2.
Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.
Chứng minh nhận xét 3. Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk.
- Phép đồng dạng tỉ số k biến 2 điểm M, N thành 2 điểm M',N' sao cho M'N' = kMN
- Phép đồng dạng tỉ số b biến 2 điểm M',N' thành 2 điểm M'',N''sao cho M''N'' = pM'N'
⇒ M''N'' = pkMN
Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk
Số phát biểuđúng:
1. Qua phép vị tự có tỉ số k ≠ 0 , đường thẳng đi qua tâm vị tự sẽ biến thành chính nó
2. Qua phép vị tự có tỉ số k ≠ 0 , đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.
3. Qua phép vị tự có tỉ số k ≠ 1 , không có đường tròn nào biến thành chính nó.
4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.
5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó
6. Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với hệ số k
7. Trong phép vị tự tâm O, tỉ số k, nếu k < 0 thì điểm M và ảnh của nó ở về hai phía đối với tâm O.
8. Mọi phép dời hình đều là phép đồng dạng với tỉ số k = 1
9. Phép hợp thành của một phép vị tự tỉ số k và một phép đối xứng tâm là phép đồng dạng tỉ số
10. Hai đường tròn bất kì luôn có phép vị tự biến đường này thành đường kia
11. Khi k = 1 , phép vị tự là phép đồng nhất
12. Phép vị tự biến tứ giác thành tứ giác bằng nó
13. Khi k = 1, phép đồng dạng là phép dời hình
14. Phép đối xứng tâm là phép đồng dạng tỉ số k = 1
A.9
B.10
C.11
D.12
Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó
Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.
A.(8; -3)
B. (-8;3)
C. (-8;-3)
D. (3;8)
V V ( I ; - 2 ) ( M ( - 1 ; 0 ) ) = M ' ( 8 ; 3 ) ; Đ O x ( M ' ) = M " ( 8 ; - 3 )
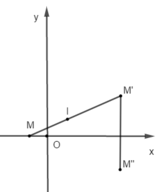
Đáp án A
Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p thì ta được phép đồng dạng có tỉ số
A. p k
B. p – k
C. p + k
D. p.k
Câu 1. Cho đoạn thẳng AB có trung điểm là I. a) Tìm ảnh của điểm B qua phép vị tự t hat a mA tỉ số k = 1/2 b)Tìm ảnh của điểm B qua phép vị tự tâm I tỉ số k = - 1 c) Tìm ảnh của điểm A qua phép vị tự tâm B tỉ số k = - 2
Trong mặt phằng Oxy, cho điểm M(2;4). Phép đồng dạng là hợp thành của phép vị tự tâm O ( 0 ; 0 ) tỉ số k = 1 2 và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào sau đây?
A. M ' ( − 1 ; 2 ) .
B. M ' ( − 2 ; 4 ) .
C. M ' ( 1 ; − 2 ) .
D. M ' ( 1 ; 2 ) .
Đáp án A.
Ta có V O ; 1 2 ( M ) = M ' ⇔ O M ¯ ' = 1 2 O M ¯
⇔ x M ' = 1 2 x M = 1 y M ' = 1 2 y M = 2 → M ' ( 1 ; 2 ) .
Trong mặt phằng Oxy, cho điểm M(2;4). Phép đồng dạng là hợp thành của phép vị tự tâm O(0;0) tỉ số k = 1 2 và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào sau đây?
A. M ' ( − 1 ; 2 ) .
B. M ' ( − 2 ; 4 ) .
C. M ' ( 1 ; − 2 ) .
D. M ' ( 1 ; 2 ) .
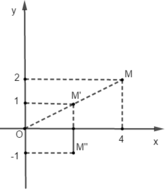
Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 1/2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.
A.(2;-1)
B. (8;1)
C.(4;-2)
D. (8;4)
V ( 0 ; 1 / 2 ) ( M ( 4 ; 2 ) ) = M ' ( 2 ; 1 ) ; Đ O x ( M ' ( 2 ; 1 ) ) = M " ( 2 ; - 1 ) .
Đáp án A.
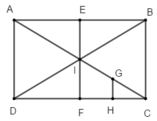
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
A. AIFD
B. BCFI
C. CIEB
D. DIEA
V ( C ; 2 ) ( I G H F ) = ( A I F D ) ; Đ I ( A I F D ) = C I E B .
Đáp án C.