chữ nhật

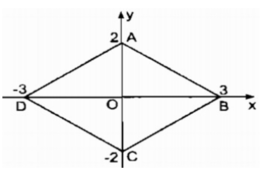
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)

⇒ OA = OC

B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)

⇒ OB = OD

Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Lại có: Ox ⊥ Oy hay AC ⊥ BD.

Vậy tứ giác ABCD là hình thoi

Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:

A B 2 = O A 2 + O B 2

A B 2 = 2 2 + 3 2  = 4 + 9 = 13

AB = 13

Vậy chu vi của hình thoi bằng 4 13

Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)

⇒ OA = OC

B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)

⇒ OB = OD

Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Lại có: Ox ⊥ Oy hay AC ⊥ BD.

Vậy tứ giác ABCD là hình thoi

Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:

AB²=OA²+OB²

AB²=4²+3² = 16 + 9 = 25

AB = √25

Vậy chu vi của hình thoi bằng 4√25

Bài 1) 

Trên AD lấy E sao cho AE = AB 

Xét ∆ACE và ∆ACB ta có : 

AC chung 

DAC = BAC ( AC là phân giác) 

AB = AE (gt)

=> ∆ACE = ∆ACB (c.g.c)

=> CE = CB (1)

=> AEC = ABC = 110°

Mà AEC là góc ngoài trong ∆EDC 

=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)

=> ECD = 110 - 70 

=> EDC = 40°

Xét ∆ EDC : 

DEC + EDC + ECD = 180 °

=> CED = 180 - 70 - 40 

=> CED = 70° 

=> CED = EDC = 70° 

=> ∆EDC cân tại C 

=> CE = CD (2)

Từ (1) và (2) :

=> CB = CD (dpcm)

b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°

Chọn A

câu 34:A

Câu 34: Cho tứ giác ABCD có góc  A= 75⁰,B= 105⁰ , C= 80⁰Khi đó số đo của  góc D bằng :

A. 100 ⁰         B. 105⁰                    C. 75⁰                             D.  80⁰

a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)

<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)

<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)

<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0

<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)

=>a=b=c=d

=> ABCD là hình thoi

\(\widehat{B}=360^0-190^0-2\cdot73^0=24^0\)