Tính độ dài x, y trong các hình bên
Tính độ dài x, y trong các hình bên
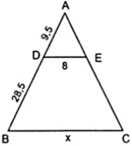
Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58
Tính độ dài x, y trong các hình bên
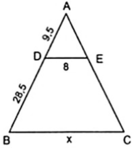
Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = 8.28,5/9,5 = 456/19 ≈ 31,58
Tính độ dài x, y trong các hình bên
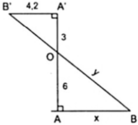
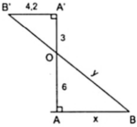
Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
O B 2 = A B 2 + O A 2 ⇒ y = 8 , 4 2 + 6 2 ≈ 10 , 32
Tính các độ dài x, y trong hình bên:
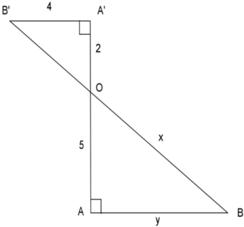
A. x = 2 5 , y = 10
B. x = 10 5 , y = 9
C. x = 6 5 , y = 10
D. x = 5 5 , y = 10
Áp dụng định lý Py-ta-go cho tam giác vuông OA’B’, ta có: O A ’ 2 + A ’ B ’ 2 = O B ' 2
⇔ 2 2 + 4 2 = O B ’ 2 ⇔ O B ' 2 = 20 ⇒ O B ’ = 20
A’B’ ⊥ AA’, AB ⊥ AA’ => A’B’// AB
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-lét, ta có: O A ' O A = O B ' O B = A ' B ' A B
⇒ 20 x = 2 5 4 y = 2 5 ⇒ x = 5 20 2 = 5 5 y = 4.5 2 = 10
Vậy x = 5 5 , y = 10
Đáp án: D
Trong hình bên có DE song song FH song song BC. Tìm các độ dài x, y
BẠN ƠI KHÔNG CÓ HÌNH
Cho hình vẽ bên
Cho biết MN // BC, AB =25cm, BC = 45cm, AM = 16cm, AN =10cm
Tính độ dài x, y của các đoạn thẳng MN,AC.
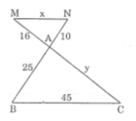
Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét suy ra:
Suy ra: 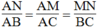 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
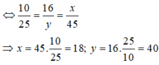
Tính các độ dài x, y trong hình 14.
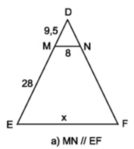
+ Hình 14a)
Ta có: MN // EF
⇒ 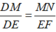 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
Mà DM = 9,5 ; DE = DM + ME = 9,5 + 28 = 37,5 ; MN = 8 ; EF = x
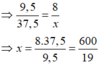
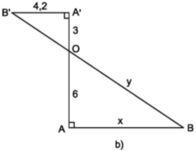
+ Hình 14b)
Ta có: A’B’ ⊥ AA’; AB ⊥ AA’ ⇒ A’B ‘ // AB
⇒ 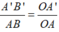 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
Mà OA’ = 3 ; OA = 6 ; A’B’ = 4,2 ; AB = x
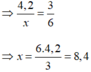
Áp dụng định lý Pytago trong tam giác OAB vuông tại A ta có:
OA2 + AB2 = OB2
Mà OA = 6; AB = x = 8,4 nên
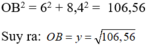
Tính các độ dài \(x,y\) trong Hình 23.
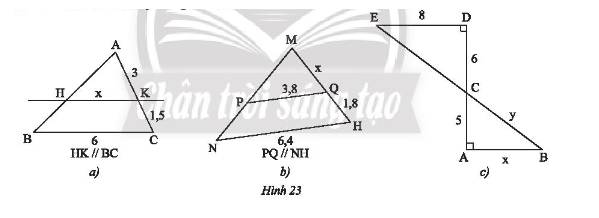
a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)
Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \Rightarrow \frac{x}{6} = \frac{3}{{4,5}}\). Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MH = MQ + QH = x + 1,8\)
Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}} \Rightarrow \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\). Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)
\( \Leftrightarrow 6,4x = 3,8x + 6,84\)
\( \Leftrightarrow 6,4x - 3,8x = 6,84\)
\( \Leftrightarrow 2,6x = 6,84\)
\( \Leftrightarrow x = 6,84:2,6\)
\( \Leftrightarrow x = \frac{{171}}{{65}}\).
Vậy \(x = \frac{{171}}{{65}}\).
c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right. \Rightarrow DE//AB\) (quan hệ từ vuông góc đến song song).
Xét \(\Delta CDE\) vuông tại \(D\) ta có:
\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)
\( \Leftrightarrow {8^2} + {6^2} = E{C^2}\)
\( \Leftrightarrow E{C^2} = 100\)
\( \Leftrightarrow EC = 10\)
Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:
\(\left\{ \begin{array}{l}\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \Rightarrow \frac{5}{6} = \frac{x}{8}\\\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \Rightarrow \frac{5}{6} = \frac{y}{{10}}\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).
Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).
Bạn hoàng dùng một tờ giấy hình chữ nhật có chiều dài 80cm, chiều rộng 60cm để trang trí, bên trong bạn vẽ một hình thoi. Em hãy tính độ dài các cạnh hình thoi bên trong?