Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào?

Những câu hỏi liên quan
Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào ?

Gọi E và F lần lượt là trung điểm của AB và AC.
Ta sẽ chứng minh ba điểm E, I, F thẳng hàng.
Do E, I lần lượt là trung điểm của AB và AM nên EI là đường trung bình của tam giác ABM. Suy ra:
EI \\ BM suy ra EI // BC. (1)
Do I, F lần lượt là trung điểm của AC và AM nên IF là đường trung bình của tam giác AMC.
Suy ra: IF // MC suy ra FI // BC. (2)
Từ (1) và (2) ta có EI và FI cùng song song với BC nên ba điểm E, F, I thẳng hàng.
Do E, F cố định nên khi M khi di chuyển trên BC thì I di chuyển trên EF.
Đúng 0
Bình luận (0)
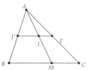
Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên cạnh BC thì trung điểm I của đoạn thẳng AM di chuyển trên đường nào?
Khi M º B thì I là trung điểm của AC. Vậy khi I di chuyển trên đoạn AB thì M di chuyển trên đoạn thẳng I''I' là đường trung bình của DABC (với I' và I'' lần lượt là trung điểm của AC và AB)
Đúng 0
Bình luận (0)
Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên
cạnh BC thì trung điểm I của đoạn thẳng AM di chuyển trên đường nào?
Khi M º B thì I là trung điểm của AC. Vậy khi I di chuyển trên đoạn AB thì M di chuyển trên đoạn thẳng I''I' là đường trung bình của DABC (với I' và I'' lần lượt là trung điểm của AC và AB)

Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm M di chuyển trên BC, goi I la trung điểm của A. Điểm I di chuyển trên đường nào.
Cho tam giác ABC vuông tại A. Điểm D trên cạnh BC, vẽ DM vuông góc với AB tại M, DN vuông góc với AC tại N.
a) Tứ giác AMDN là hình gì? Vì Sao? Tính diện tích tứ giác AMDN biết AM = 3cm, AD = 5cm.
b) Gọi AH là đường cao của tam giác ABC. Tính góc MHN.
c) Khi điểm D di chuyển trên cạnh BC thì trung điểm I của MN di chuyển trên đoạn thẳng nào?
Giải thích các bước giải:
a. Vì DM⊥AB⇒ˆDMA=90oDM⊥AB⇒DMA^=90o,
DN⊥AC⇒ˆDNA=90oDN⊥AC⇒DNA^=90o,
ΔABC⊥A⇒ˆA=90oΔABC⊥A⇒A^=90o
⇒◊AMDN⇒◊AMDN là hình chữ nhật.
Áp dụng định lý Pitago vào ΔAMD⊥M,AM=3cm,AD=5cmΔAMD⊥M,AM=3cm,AD=5cm có:
MD=√AD2−AM2=4cmMD=AD2−AM2=4cm
⇒SAMDN=AM.DM=12cm2⇒SAMDN=AM.DM=12cm2
b. Gọi AD∩MN=E⇒EAD∩MN=E⇒E là trung điểm AD, MN
Mà AH⊥BCAH⊥BC
ΔAHD⊥H,EΔAHD⊥H,E là trung điểm cạnh huyền ADAD
⇒EH=EA=ED=EM=EN⇒EH=EA=ED=EM=EN
⇒ΔMHN⇒ΔMHN vuông tại HH
⇒ˆMHN=90o⇒MHN^=90o
c. Gọi G,IG,I là trung điểm AB,ACAB,AC suy ra GIGI là đường trung bình của ΔABCΔABC
⇒GI//BC⇒GI//BC
⇒GE,EI⇒GE,EI là đường trung bình ΔABD,ΔADC⇒GE//BD,EI//DCΔABD,ΔADC⇒GE//BD,EI//DC hay GE,EI//BCGE,EI//BC
⇒E∈GI⇒E∈GI
⇒⇒ Trung điểm EE của MNMN di chuyển trên đường trung bình ΔABCΔABC.
bài 1: cho tam giác ABC vuông cân tại A.M di chuyển trên đường cao AH qua E kẻ đường thẳng vuoonh góc với BM cắt BC tại E.hỏi khi M di chuyển trên AH thì trung điểm I của ME chỵ trên đường nàobài 2:cho tam giác abc cạnh BC a, các trung tuyến BD, CE. lấy M,N trên BC sao cho BMMNNC. gọi I là giao điểm của AM và BD.J là giao điểm của AN và EC.tính IJ theo abài 3: tam giác ABC. O là điểm cách dều 3 cạnh.trên tia BC lấy M sao cho BMBA. trên tia CB lấy N sao cho CN CA. gọi D,E,F là hình chiếu của O t...
Đọc tiếp
bài 1: cho tam giác ABC vuông cân tại A.M di chuyển trên đường cao AH qua E kẻ đường thẳng vuoonh góc với BM cắt BC tại E.hỏi khi M di chuyển trên AH thì trung điểm I của ME chỵ trên đường nào
bài 2:cho tam giác abc cạnh BC =a, các trung tuyến BD, CE. lấy M,N trên BC sao cho BM=MN=NC. gọi I là giao điểm của AM và BD.J là giao điểm của AN và EC.tính IJ theo a
bài 3: tam giác ABC. O là điểm cách dều 3 cạnh.trên tia BC lấy M sao cho BM=BA. trên tia CB lấy N sao cho CN =CA. gọi D,E,F là hình chiếu của O trên BC,CA,AB.chứng minh NE=NF
cho tam giác ABC gọi D,M,E theo thứ tự là trung điểm của AB,BC,CA
a) chứng minh tứ giác ADME là hình bình hành
b) tam giác ABC có điều kiện gì thì tứ giác ADME là hình chữ nhật
c) khi M di chuyển trên cạnh BC thì trung điểm J của AM di chuyển trên đường nào+
Cho tam giác ABC vuông tại A. Lấy M là1 điểm bất kỳ thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE
a) CM: 3 điểm A,O,M thẳng hàng
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
c)Điểm M ở vị trí nào trên cạnh BC thì điểm AM có độ dài nhỏ nhất?
Bạn chỉ cần chứng minh AEDM là HCN ;O là trung điểm của DE =>O cũng là trung điểm của AM =>O,M,A thẳng hàng
b,
Gọi P ,Q lần lượt là trung điểm của AB,AC
=> giới hạn :
*Khi M trùng với B=> O trùng với P
*Khi M trùng với C=> O trùng với Q
=> I thuộc PQ
c,
Kẻ đường cao AH
Khi M trùng với H thì AM ngắn nhất (quan hệ đường vuông góc và đường xiên)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE. a) Chứng minh rằng ba điểm A, O, M thẳng hàng. b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào? c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?
Đọc tiếp
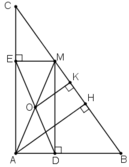
Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
a) Chứng minh rằng ba điểm A, O, M thẳng hàng.
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?
a) Tứ giác ADME có: 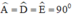
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.
Đúng 1
Bình luận (0)














