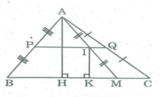
Kẻ AH ⊥ BC,IK ⊥ BC ⇒ AH // IK
Trong ∆ AHM, ta có:
AI = IM (gt)
IK // AH ( chứng minh trên)
Suy ra IK là đường trung bình của ∆ AHM
⇒ IK = 1/2 AH
∆ ABC cố định nên AH không thay đổi ⇒ IK = 1/2 AH không đổi.
I thay đổi cách BC một khoảng bằng AH/2 không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằng AH/2
Khi M trùng với điểm B thì I trùng với điểm P là trung điểm của AB.
Khi M trùng với điểm C thì I trùng với điểm Q là trung điểm của AC.
Vậy khi M di chuyển trên cạnh BC của ∆ ABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của ∆ ABC









