Lập phương trình mặt phẳng (P) chứa hai đường thẳng: d: x = - 2 - t y = 1 + 4 t z = 1 - t và d': x = - 1 + t ' y = - 3 + 4 t ' z = 2 - 3 t '
Những câu hỏi liên quan
Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng: d:
x
+
2
-
1
y
-
1
4
z
-...
Đọc tiếp
Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng: d: x + 2 - 1 = y - 1 4 = z - 1 - 1
Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương a → (−1; 4; −1)
Ta có: MI → (1; −2; 0), chọn n P → = MI → ∧ a → = (2; 1; 2)
Phương trình của (P) là: 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0
Đúng 0
Bình luận (0)
Lập phương trình mặt phẳng (P) chứa đường thẳng d:
x
-
2
-
t
y
1
+
4
t...
Đọc tiếp
Lập phương trình mặt phẳng (P) chứa đường thẳng d: x = - 2 - t y = 1 + 4 t z = 1 - t và song song với d 1 x - 1 1 = y - 1 4 = z - 1 - 3
Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a → (−1; 4; −1)
Đường thẳng d1 đi qua N(1; 1; 1) có vecto chỉ phương là b → (1; 4; −3)
Ta có: MN → (3; 0; 0); a → ∧ b → = (−8; −4; −8) nên MN → ( a → ∧ b → ) ≠ 0, suy ra d và d 1 chéo nhau. Do đó (P) là mặt phẳng đi qua M(-2; 1; 1) có vecto pháp tuyến bằng a → ∧ b →
Phương trình của (P) là: –8(x + 2) – 4(y – 1) – 8(z – 1) = 0 hay 2x + y + 2z + 1 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d:
x
2
+
3
t
y
-
3
+
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d: x = 2 + 3 t y = - 3 + t z = 4 - 2 t và d': x - 4 3 = y + 1 1 = z - 2 . Phương trình nào dưới đây là phương trình đường thẳng thuộc mặt phẳng chứa d và d’, đồng thời cách đều hai đường thẳng đó.
A. x - 3 3 = y + 2 1 = z - 2 - 2
B. x + 3 3 = y + 2 1 = z + 2 - 2
C. x + 3 3 = y - 2 1 = z + 2 - 2
D. x - 3 3 = y - 2 1 = z - 2 - 2
Đáp án A
Vì hai đường thẳng d và d’ song song với nhau nên đường thẳng a cần tìm cũng song song với 2 đường thẳng nên a nhận u ⇀ =(3;1;-2) làm vecto chỉ phương.
Gọi A(2;-3;4) ∈ d ⇒ phương trình mặt phẳng (P) qua A vuông góc với d là: 3x+y-2z+5=0
Giao điểm H của (P) và d’ là H 4 7 ; - 15 7 ; - 16 7 . khi đó trung điểm của AH là I 9 7 ; - 18 7 ; 6 7
Thay tọa độ điểm I vào xem phương trình nào thỏa mãn.
Đúng 0
Bình luận (0)
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:
x
12
+
4
t
y
9
+
3
t
z...
Đọc tiếp
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Viết phương trình mặt phẳng β chứa điểm M và vuông góc với đường thẳng d.
(β) vuông góc với d
⇒ (β) nhận vtcp của d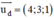 
là 1 vtpt.
(β) đi qua M(0; 0; -2)
⇒ (β): 4x + 3y + z + 2 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, coh đường thẳng d là giao tuyến của hai mặt phẳng
P
:
x
+
y
+
z
3
và
P
:
x
-
y
+
z
5
. Mặt phẳng
α
chứa đường thẳng d và đi qua gốc tọa độ có phương trình là A.
x
+
4
y
+
z
0
B....
Đọc tiếp
Trong không gian Oxyz, coh đường thẳng d là giao tuyến của hai mặt phẳng P : x + y + z = 3 và P : x - y + z = 5 . Mặt phẳng α chứa đường thẳng d và đi qua gốc tọa độ có phương trình là
A. x + 4 y + z = 0
B. 5 x + 4 y + z = 0
C. x - 4 y + z = 0
D. 5 x - 4 y + z = 0
Chọn đáp án A.
Cách 1: Đường thẳng d có một vectơ chỉ phương là
Cách 2: Vì mặt phẳng α chứa đường thẳng d nên α có phương trình
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
:
x
+
y
-
z
-
2
0
và đường thẳng
d
:
x
+
1
2
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + y - z - 2 = 0 và đường thẳng d : x + 1 2 = y - 1 1 = z - 2 1 Phương trình nào dưới đây là phương trình mặt phẳng chứa đường thẳng (d) và vuông góc với mặt phẳng α
A. x+y-z+2=0
B. 2x-3y-z+7=0
C. x+y+2z-4=0
D. 2x-3y-z-7=0
Đáp án B
Phương pháp giải:
Ứng dụng của tích có hướng để tìm vectơ pháp tuyến của mặt phẳng. Phương trình mặt phẳng đi qua M ( x 0 ; y 0 ; z 0 ) và có VTPT
Lời giải:
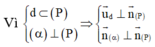
Vậy phương trình mặt phẳng (P): 2x-3y-z+7=0
Đúng 0
Bình luận (0)
Trong không gian Oxyz, có đường thẳng d là giao tuyến của hai mặt phẳng
P
:
x
+
y
+
z
3
và
Q
:
x
-
y
+
z
5
. Mặt phẳng (α) chứa đường thẳng d và đi qua gốc tọa độ có phương trình là A.
x
+
4
y
+
z
0
B....
Đọc tiếp
Trong không gian Oxyz, có đường thẳng d là giao tuyến của hai mặt phẳng P : x + y + z = 3 và Q : x - y + z = 5 . Mặt phẳng (α) chứa đường thẳng d và đi qua gốc tọa độ có phương trình là
A. x + 4 y + z = 0
B. 5 x + 4 y + z = 0
C. x - 4 y + z = 0
D. 5 x - 4 y + z = 0
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d:
x
1
y
-
2
z
+
1
1
và d
x
-
1
-
2
)...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: x 1 = y - 2 = z + 1 1 và d'= x - 1 - 2 ) = y - 2 4 = z 2 . Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’
A. Không tồn tại (Q)
B. (Q): y-2z-2= 0
C. (Q): x-y-2= 0
D. (Q):-2y+4z+1= 0
Cho đường thẳng
d
:
x
-
1
1
y
+
1
2
z
-
1
. Viết phương trình mặt phẳng (P) chứa đường thẳng d, vuông góc với mặt phẳng (Oxy). A.
2
x
+
y
+
3
0...
Đọc tiếp
Cho đường thẳng d : x - 1 1 = y + 1 2 = z - 1 . Viết phương trình mặt phẳng (P) chứa đường thẳng d, vuông góc với mặt phẳng (Oxy).
A. 2 x + y + 3 = 0
B. 2 x - y - 3 = 0
C. 2 x - y + 3 = 0
D. - 2 x + y + 3 z = 0