Tam thức 3 x 2   +   x   +   5 có biệt thức Δ = -59 < 0 và hệ số a = 3 > 0

    Vậy  3 x 2   +   x   +   5 > 0, ∀x

a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai

          \(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)

b) Biểu thức \(g\left( x \right) =  - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai

c) Biểu thức \(h\left( x \right) =  - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai

          \(h\left( 1 \right) =  - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2  - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)

f(x) = (2x – 3)(x + 5) = 2x2 + 7x – 15

Tam thức f(x) = 2x2 + 7x – 15 có hai nghiệm phân biệt x1 = 3/2; x2 = –5, hệ số a = 2 > 0.

Ta có bảng xét dấu:

Vậy f(x) > 0 khi x ∈ (–∞; –5) ∪ (3/2; +∞)

f(x) = 0 khi x = –5 ; x = 3/2

f(x) < 0 khi x ∈ (–5; 3/2)

a) Ta có \(a =  - 2 < 0\), \(b = 4 =  > b' = 2\) và \(c =  - 5\)

\(\Delta ' = {2^2} - \left( { - 2} \right).\left( { - 5} \right) =  - 6 < 0\)

=>\(f\left( x \right)\) cùng dấu âm với hệ số a.

=> \(f\left( x \right) < 0\forall x \in \mathbb{R}\)

b) Ta có: \(a =  - 1,b = 6,c =  - 9 =  > b' = 3\)

\(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)

\(\frac{{ - b}}{{2a}} = \frac{{ - b'}}{a} = 3\)

=> \(f\left( x \right)\) cùng dấu âm với hệ số a với mọi \(x \in \mathbb{R}\backslash \left\{ 3 \right\}\)

=> \(f\left( x \right) < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)

a) \(f(x) = 3{x^2} - 4x + 1\)có \(\Delta  = 4\)>0, \(a = 3 > 0\)và có hai nghiệm phân biệt \({x_1} = 1;{x_2} = \frac{1}{3}\). Do đó ta có bảng xét dấu \(f(x)\):

Suy ra \(f(x) > 0\)với mọi \(x \in \left( { - \infty ;\frac{1}{3}} \right) \cup \left( {1; + \infty } \right)\) và \(f(x) < 0\)với mọi \(x \in \left( {\frac{1}{3};1} \right)\)

b) \(g(x) = {x^2} + 2x + 1\) có \(\Delta  = 0\) và a=1>0 nên \(g(x)\)có nghiệm kép \(x =  - 1\) và \(g(x) > 0\)với \(x \ne  - 1\)

c) \(h(x) =  - {x^2} + 3x - 2\) có \(\Delta  = 1 > 0\), \(a =  - 1\)

Suy ra \(h(x) > 0\) với mọi \(x \in (1;2)\)và \(h(x) < 0\)với mọi \(x \in ( - \infty ;1) \cup (2; + \infty )\)

d) \(k(x) =  - {x^2} + x - 1\) có \(\Delta  =  - 3\), a=-1

Suy ra \( k(x) >0 \)với mọi \(x \in \mathbb{R}\)

a) \(f\left( x \right) = 2{x^2} - 3x - 2\) có \(\Delta  = 25 > 0\), hai nghiệm phân biệt là \({x_1} =  - \frac{1}{2};{x_2} = 2\)

và \(a = 2 > 0\)

Ta có bảng xét dấu như sau:

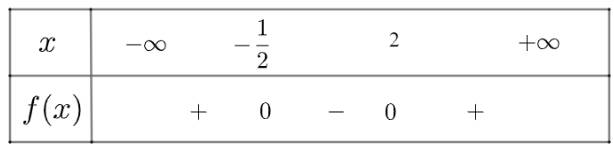
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \frac{1}{2},2} \right)\) và dương trong hai khoảng

 \(\left( { - \infty , - \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)

b) \(g\left( x \right) =  - {x^2} + 2x - 3\) có \(\Delta  = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) =  - 8 < 0\) và \(a =  - 1 < 0\)

Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)

Tham khảo:

Tam thức bậc hai \(f\left( x \right) =  - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} =  - 4,{x_2} = 2\) và hệ số \(a =  - 1 < 0\).

Ta có bảng xét dấu \(f\left( x \right)\) như sau:

a) \(f(x) =  - 3{x^2} + x - \sqrt 2 \)có \(\Delta  = 1 - 12\sqrt 2  < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)

b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta  = 0\)và a=1>0 nên g(x) có nghiệm kép \(x =  - 4\) và g(x) >0 với mọi \(x \ne  - 4\)

c) \(h(x) =  - 2{x^2} + 7x - 3\) có \(\Delta  = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)

Do đó ta có bảng xét dấu h(x)

Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)

a) \(f\left( x \right) = 6{x^2} + 41x + 44\) có \(\Delta  = 625 > 0\), có hai nghiệm phân biệt là \({x_1} =  - \frac{{11}}{2},{x_2} =  - \frac{4}{3}\) và có \(a = 6 > 0\)

Ta có bảng xét dấu \(f\left( x \right)\)như sau:

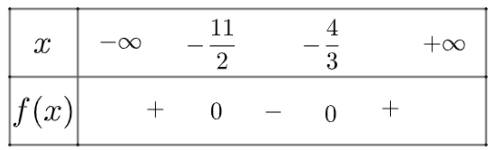
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right) \cup \left( { - \frac{4}{3}; + \infty } \right)\) và âm trong khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\)

b) \(g\left( x \right) =  - 3{x^2} + x - 1\) có \(\Delta  =  - 11 < 0\) và có \(a =  - 3 < 0\)

Ta có bảng xét dấu như sau

Vậy \(g\left( x \right)\)luôn âm với mọi \(x \in \mathbb{R}\)

c) \(h\left( x \right) = 9{x^2} + 12x + 4\) có \(\Delta  = 0\), có nghiệm kép là \({x_1} = {x_2} =  - \frac{2}{3}\) và có \(a = 9 > 0\)

Ta có bảng xét dấu của \(h\left( x \right)\) như sau:

Vậy \(h\left( x \right)\) luôn dương khi \(x \ne  - \frac{2}{3}\)

f(x) = x2 – 5x +4

f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0