1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)

       \(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)

       \(\Leftrightarrow2\widehat{C}=90^o\)

      \(\Leftrightarrow\widehat{C}=45^o\)

 \(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)

\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)

2,

Vì tam giác ABC vuông tại A

=> ^B + ^C = 90^o

Vì BM là phân giác ^ABC 

=>^B₁ = \(\frac{\widehat{ABC}}{2}\)

Tương tự ^C₁ = \(\frac{\widehat{ACB}}{2}\)

\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)

Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)

`hatA+hatB+hatC=180^o`

mà `hatA=hatB+hatC `

`=>hatA+hatA=180^o`

`=>2hatA=180^o`

`=>hatA=90^o`

`+)hat{BOC}=180-  (hat{OBC}+hat{OCB})`

 .vì o là giao điểm của 3 đường phân giác

`=>2(hat{BOC}+hat{OCB})=hatA=90^o`

`=>hat{BOC}=180^o-90^o/2=180^o-45^o=135^o`

_135⁰

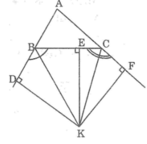
Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.

Kẻ KE ⊥ BC, KF ⊥ AC, KD ⊥ AB

Vì K nằm trên phân giác của ∠(CBD) nên:

KD = KE (tính chất tia phân giác) (1)

Vì K nằm trên tia phân giác của ∠(BCF) nên:

KE = KF (tính chất tia phân giác) (2)

Từ (1) và (2) suy ra: KD = KF

Điểm K nằm trong ∠(BAC) cách đều 2 cạnh AB và AC nên K nằm trên tia phân giác của ∠(BAC) .

Ôi thần linh ơi, bài hình ah

thần linh ơi bài hình

Bài hình thì chắc mình chịu

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có 

góc B chung

Do đó ΔHBA\(\sim\)ΔABC

b: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

c: Xét ΔAHB vuông tại H có HD là đường cao

nên \(AD\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HE là đường cao

nên \(AE\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

hay AD/AC=AE/AB

=>ΔADE\(\sim\)ΔACB

Tam giác ABC có chu vi bằng 74cm, AC là cạnh lớn nhất. Đường phân giác của góc A chia cạnh BC thành hai đoạn tỉ lệ với 2:3; đường phân giác của góc C chia cạnh AB thành hai đoạn tỉ lệ với 4:5. Tính độ dài các cạnh của tam giác ABC. 

AB + BC + AC = 74 (*) 
Trong ∆ ABC phân giác AD → AB/AC = DB/DC = 2/3 (AC > AB) 
→ AB = 2/3 . AC (1) , tương tự với phân giác CE ta suy ra 
BC = 4/5 . AC (2) . Thế tất cả vào (*) ta được: 
2/3 . AC + 4/5 . AC + AC = 74 → 37AC/15 = 74 → AC = 30cm 
thế vào (1) và (2) ta được AB = 10cm, BC = 24cm

Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath

Tham khảo bài 3 tại link trên nhé!