Giải các phương trình sau trên tập số phức:
(7 - 3i)z + (2 + 3i) = (5 - 4i)z
Những câu hỏi liên quan
Giải các phương trình sau trên tập số phức:
a)(5 − 7i) + √3x = (2 − 5i)(1 + 3i);
b) 5 – 2ix = (3 + 4i)(1 – 3i).
Giải các phương trình sau trên tập số phức: 5 – 2ix = (3 + 4i)(1 – 3i).
Giải các phương trình sau trên tập số phức :
a) \(\left(3+2i\right)z-\left(4+7i\right)=2-5i\)
b) \(\left(7-3i\right)z+\left(2+3i\right)=\left(5-4i\right)z\)
c) \(z^2-2z+13=0\)
d) \(z^4-z^2-6=0\)
a) (3 + 2i)z – (4 + 7i) = 2 – 5i
⇔(3+2i)z=6+2i
<=> z = \(\dfrac{\text{6 + 2 i}}{\text{3 + 2 i}}\) = \(\dfrac{22}{13}\) - \(\dfrac{6}{13}\)i
b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z
⇔(7−3i−5+4i)=−2−3i
⇔z= \(\dfrac{\text{− 2 − 3 i}}{\text{2 + i}}\) = \(\dfrac{-7}{5}\) - \(\dfrac{4}{5}i\)
c) z2 – 2z + 13 = 0
⇔ (z – 1)2 = -12 ⇔ z = 1 ± 2 √3 i
d) z4 – z2 – 6 = 0
⇔ (z2 – 3)(z2 + 2) = 0
⇔ z ∈ { √3, - √3, √2i, - √2i}
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập số phức:
(3 + 4i)x + ( 1 – 3i) = 2 + 5i
Giải các phương trình sau trên tập số phức :
a) \(\left(3+4i\right)z+\left(1-3i\right)=2+5i\)
b) \(\left(4+7i\right)z-\left(5-2i\right)=6iz\)
a) (3 + 4i)z = (2 + 5i) – (1 – 3i) = 1 + 8i
Vậy z=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45iz=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45i
b) (4 + 7i)z – (5 – 2i) = 6iz ⇔ (4 + 7i)z – 6iz = 5 – 2i
⇔ (4 + i)z = 5 – 2i
⇔z=5−2i4+i=(5−2i)(4−i)17⇔z=1817−1317i
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập số phức:
a) (3 + 4i)x = (1 + 2i)(4 + i)
b) 2ix + 3 = 5x + 4i
c) 3x(2 – i) + 1 = 2ix(1 + i) + 3i
a) (3 + 4i)x = (1 + 2i)(4 + i)
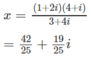
b) 2ix + 3 = 5x + 4i
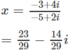
c) 3x(2 – i) + 1 =2ix(1 + i) + 3i
Đúng 0
Bình luận (0)
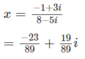
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Trên mặt phẳng phức, tập hợp các số phức
z
x
+
y
i
x
,
y
∈
ℝ
thỏa mãn
z
+
2
+
i
z
¯
-
3
i...
Đọc tiếp
Trên mặt phẳng phức, tập hợp các số phức z = x + y i x , y ∈ ℝ thỏa mãn z + 2 + i = z ¯ - 3 i là đường thẳng có phương trình
A. y = x + 1
B. y = - x + 1
C. y = - x - 1
D. y = x - 1
Giải các phương trình sau trên tập số phức :
a) \(\left(5-7i\right)+\sqrt{3}x=\left(2-5i\right)\left(1+3i\right)\)
b) \(5-2ix=\left(3+4i\right)\left(1-3i\right)\)