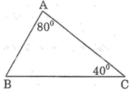
So sánh các cạnh của tam giác ABC biết rằng ∠A = 80o, ∠C = 40o
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính ∠(BIC) biết rằng: ∠B = 80o,∠C = 40o
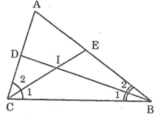
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o
Cho tam giác ABC có ∠ A = 80 o , và C cắt nhau tại I.
b.Giả sử góc ∠ B = 30 o . So sánh các cạnh của tam giác ABC
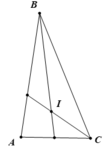
b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )
Cho tam giác ABC cân ở A có ∠ B = 40 o . So sánh các cạnh của tam giác ABC.
A. AB = AC > BC
B. AB = AC < BC
C. AB < AC = BC
D. AB = AC = BC
Tam giác ABC cân tại A có ∠C = ∠B = 40o, ∠A = 100o
Vì B = C < A ⇒ AC = AB < BC. Chọn B
CAN GAP GAP
Cho tam giác ABC có A = 80o, B = 60o, C = 40o. Kẻ phân giác BD của tam giác.
Chứng minh rằng AB + AD = BC.
Trên BC lấy điểm E sao cho \(AB=BE\)
Dễ dàng chứng minh được \(\Delta ABD=\Delta EBD\left(c.g.c\right)\)
Do đó \(\widehat{BAC}=\widehat{BED}=80^0\)
Mà \(\widehat{BED}\) là góc ngoài tam giác DEC
\(\Rightarrow\widehat{BED}=\widehat{EDC}+\widehat{BCA}\\ \Rightarrow80^0=\widehat{EDC}+40^0\\ \Rightarrow\widehat{EDC}=40^0\Rightarrow\widehat{EDC}=\widehat{ECD}\left(=40^0\right)\\ \Rightarrow\Delta EDC.cân.tại.E\Rightarrow DE=EC\)
Vậy \(AB+AD=BE+EC=BC\)
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
b.Giả sử góc ∠ B = 30 o . So sánh các cạnh của tam giác ABC
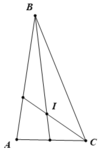
b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )
So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng 40o.
Theo giả thiết, tam giác cân này có một góc ngoài bằng 40o nên nó có một góc trong bằng 180o - 40o = 140o. Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh. Vậy cạnh đáy của tam giác cân lớn hơn hai cạnh bên của nó.
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC có ∠ A = 80 o , B = 30 o . So sánh các cạnh của tam giác ABC.
A. AB > AC > BC
B. AB > BC > CA
C. BC > AC > AB
D. CB > AB > AC
Ta có ∠C = 180o - 80o - 30o = 70o
Vì A > C > B ⇒ BC > AB > AC. Chọn D
Cho tam giác ABC có góc B= 80o, C=40o. tia phân giác của góc B cắt cạnh AC tại D. Kẻ tia DE song song với BC ( E nằm giữa A và B)
Tính góc A
A. Phần trắc nghiệm (4 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC có các góc A = 40 o , B = 25 o . So sánh các cạnh của tam giác.
A. AB > AC > BC
B. AB > BC > CA
C. BC > AC > AB
D. CB > AB > AC
Ta có: ∠C = 180o - 40o - 25o = 115o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn B