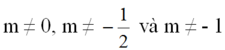Theo đề bài ta có b ≠ b' (vì 2 ≠ 1)

Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:

    a – 1 = 3 – a

=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)

Vậy với a = 2 thì hai đường thẳng song song với nhau.

Theo đề bài ta có b ≠ b' (vì 2 ≠ 1)

Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:

    a – 1 = 3 – a

=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)

Vậy với a = 2 thì hai đường thẳng song song với nhau.

Theo đề bài ta có b ≠ b' (vì 2 ≠ 1)

Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:

    a – 1 = 3 – a

=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)

Vậy với a = 2 thì hai đường thẳng song song với nhau.

a) Hàm số y=(a–1)x+a(a≠1)y=(a–1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục tung

tại điểm có tung độ bằng y = 2 nên a = 2.

b) Hàm số y=(a–1)x+a(a≠1)y=(a–1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 nên tung độ giao điểm này bằng 0.

Ta có:

0=(a–1)(–3)+a⇔–3x+3+a=0⇔–2a=–3⇔a=1,50=(a–1)(–3)+a⇔–3x+3+a=0⇔–2a=–3⇔a=1,5                                   

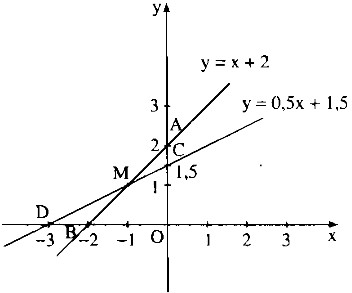
c) Khi a = 2 thì ta có hàm số: y = x + 2

Khi a = 1,5 thì ta có hàm số: y=0,5x+1,5y=0,5x+1,5

* Vẽ đồ thị của hàm số y=x+2y=x+2

Cho x = 0 thì y = 2. Ta có: A(0;2)

Cho y = 0 thì x = -2. Ta có: B(-2;0)

Đường thẳng AB là đồ thị hàm số y=x+2y=x+2.

* Vẽ đồ thị của hàm số y=0,5x+1,5y=0,5x+1,5

Cho x = 0 thì y = 1,5. Ta có: C(0;1,5)

Cho y = 0 thì x = -3. Ta có : B(-3;0)

Đường thẳng CD là đồ thị hàm số y=0,5x+1,5y=0,5x+1,5

* Tọa độ giao điểm  của hai đường thẳng .

Ta có: I thuộc đường thẳng y=x+2y=x+2 nên y1=x1+2y1=x1+2

            I thuộc đường thẳng y=0,5x+1,5y=0,5x+1,5 nên y1=0,5x1+1,5y1=0,5x1+1,5

Suy ra:

x1+2=0,5x1+1,5⇔0,5x1=–0,5⇔x1=–1x1+2=0,5x1+1,5⇔0,5x1=–0,5⇔x1=–1

x1=–1⇒y1=–1+2=1x1=–1⇒y1=–1+2=1           

Vậy tọa độ giao điểm của hai đường thẳng là I(-1;1).

a: Để hai đường thẳng song song thì a-1=3

hay a=4

a: Để hai đường thẳng y=(a-1)x+5 và y=(3-a)x+2 song song với nhau thì \(\left\{{}\begin{matrix}a-1=3-a\\5\ne2\left(đúng\right)\end{matrix}\right.\)

=>a-1=3-a

=>2a=4

=>a=2

b: Để hai đường thẳng y=kx+(m-2) và y=(5-k)x+4-m trùng nhau thì \(\left\{{}\begin{matrix}k=5-k\\m-2=4-m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2k=5\\2m=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=\dfrac{5}{2}\\m=3\end{matrix}\right.\)

Để 2 đường thẳng trùng nhau thì

\(\dfrac{a-1}{3-a}=\dfrac{2}{1}\)

ĐK: \(a\ne3\)

=> a-1=6-2a

<=>3a=7

<=>a=\(\dfrac{7}{3}\)

Vậy a=\(\dfrac{7}{3}\)thì 2 đường thẳng trên song song

a) Để 2 đường thẳng song song thì a=a',tương đương với 2=m-1. Vậy m=3 

b)Để 2 đường thẳng cắt nhau thì a#a',tương đương 2#m-1. Vậy m#3

c)Để 2 đường thẳng vuông góc với nhau thì a.a'=1,tương đương 2.(m-1)=1.Vậy m=3/2

\(1,\Leftrightarrow\left\{{}\begin{matrix}a=-3\\4\ne-1\end{matrix}\right.\Leftrightarrow a=-3\\ 2,\Leftrightarrow\left\{{}\begin{matrix}2m=m-1\\1\ne3\end{matrix}\right.\left(m\ne0;m\ne1\right)\Leftrightarrow m=-1\\ 3,\)

PTHDGD: \(x+3=mx-1\)

Mà chúng cắt tại hoành độ 1 nên \(x=1\Leftrightarrow m-1=4\Leftrightarrow m=5\)

\(5,A\left(2;4\right)\inđths\Leftrightarrow2a+2=4\Leftrightarrow a=1\Leftrightarrow y=x+2\)

PT giao Ox: \(x+2=0\Leftrightarrow x=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)

PT giao Oy: \(y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\)

Vì \(OA=OB\) nên OAB vuông cân

Vậy góc tạo bởi đths là 45⁰

Hàm số y = mx + 3 có các hệ số a = m, b = 3.

Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5

a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:

    m ≠ 0 và 2m + 1 ≠ 0 hay

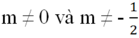
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)

Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:

    m = 2m + 1 => m = - 1

Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.

b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:

    m ≠ 2m + 1 => m ≠ -1.

Kết hợp với điều kiện trên, ta có: