Cho phương trình 3x2 + 7x + 4 = 0.
Xác định các hệ số a, b, c rồi tính a - b + c.
Những câu hỏi liên quan
Cho phương trình
3
x
2
+
7
x
+
4
0
.
a) Xác định các hệ số a, b, c rồi tính a - b + c.b) Chứng tỏ rằng
x
1
-
1
là một nghiệm của phương trình.c) Tìm nghiệm
x
2
.
Đọc tiếp
Cho phương trình 3 x 2 + 7 x + 4 = 0 .
a) Xác định các hệ số a, b, c rồi tính a - b + c.
b) Chứng tỏ rằng x 1 = - 1 là một nghiệm của phương trình.
c) Tìm nghiệm x 2 .
a) a = 3; b = 7; c = 4
⇒ a + b + c = 3 - 7 + 4 = 0
b) Thay x = -1 vào phương trình ta được:
3 . ( - 1 ) 2 + 7 . ( - 1 ) + 4 = 0
Vậy x = - 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
x 1 . x 2 = c / a = 4 / 3 ⇒ x 2 = 4 / 3 : ( - 1 ) = - 4 / 3
Đúng 0
Bình luận (0)
Cho phương trình 2x2 – 5x + 3 = 0.
Xác định các hệ số a, b, c rồi tính a + b + c.
a = 2; b = -5; c = 3
⇒ a + b + c = 2 - 5 + 3 = 0
Đúng 0
Bình luận (0)
Xác định các hệ số a, b, c ; tính biệt thức ∆ rồi tìm nghiệm của các phương trình : 4 x 2 + 4x + 1 = 0
Phương trình 4 x 2 + 4x + 1 = 0 có a = 4, b = 4, c = 1
Ta có: ∆ = b 2 – 4ac = 4 2 – 4.4.1 = 16 – 16 = 0
Phương trình có nghiệm kép :
Đúng 0
Bình luận (0)
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:
3x2 + 8x + 4 = 0;
3x2 + 8x + 4 = 0;
a = 3; b' = 4; c = 4
Δ'= (b')2 - ac = 42 - 3.4 = 4 ⇒ √(Δ') = 2
Phương trình có 2 nghiệm:
x1 = (-4 + 2)/3 = (-2)/3; x2 = (-4 - 2)/3 = -2
Đúng 0
Bình luận (0)
Cho phương trình
2
x
2
–
5
x
+
3
0
.
a) Xác định các hệ số a, b, c rồi tính a + b + c.b) Chứng tỏ rằng
x
1
1
là một nghiệm của phương trình.c) Dùng định lý Vi-ét để tìm
x
2
Đọc tiếp
Cho phương trình 2 x 2 – 5 x + 3 = 0 .
a) Xác định các hệ số a, b, c rồi tính a + b + c.
b) Chứng tỏ rằng x 1 = 1 là một nghiệm của phương trình.
c) Dùng định lý Vi-ét để tìm x 2
a) a = 2; b = -5; c = 3
⇒ a + b + c = 2 - 5 + 3 = 0
b) Thay x = 1 vào phương trình ta được:
2 . 1 2 - 5 . 1 + 3 = 0
Vậy x = 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
x 1 . x 2 = c / a = 3 / 2 ⇒ x 2 = 3 / 2
Đúng 0
Bình luận (0)
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
-3x2 + 4√6.x + 4 = 0.
Phương trình bậc hai: 
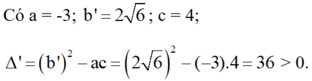
Phương trình có hai nghiệm phân biệt :
Đúng 0
Bình luận (0)
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:
a
)
3
x
2
+
8
x
+
4
0
b
)
7
x
2
−...
Đọc tiếp
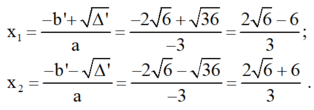
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:
a ) 3 x 2 + 8 x + 4 = 0 b ) 7 x 2 − 6 2 x + 2 = 0
a) 3 x 2 + 8 x + 4 = 0 ;
a = 3; b' = 4; c = 4
Δ ' = ( b ' ) 2 - a c = 4 2 - 3 . 4 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( - 4 + 2 ) / 3 = ( - 2 ) / 3 ; x 2 = ( - 4 - 2 ) / 3 = - 2
b) 7 x 2 - 6 √ 2 x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ ' = ( b ' ) 2 - a c = ( - 3 √ 2 ) 2 - 7 . 2 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( 3 √ 2 + 2 ) / 7 ; x 2 = ( 3 √ 2 - 2 ) / 7
Đúng 0
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7
x
2
−
2
x
+
3
0
b
)
5
x
2...
Đọc tiếp
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:
7 x 2 − 2 x + 3 = 0 b ) 5 x 2 + 2 10 x + 2 = 0 c ) 1 2 x 2 + 7 x + 2 3 = 0 d ) 1 , 7 x 2 − 1 , 2 x − 2 , 1 = 0
a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai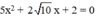 
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai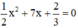 
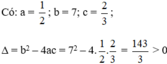
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt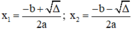 
+ Nếu Δ = 0, phương trình có nghiệm kép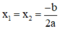 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số \(a\) và \(b\) của phương trình bậc nhất một ẩn đó.
a) \(7x + \dfrac{4}{7} = 0\);
b) \(\dfrac{3}{2}y - 5 = 4\);
c) \(0t + 6 = 0\);
d) \({x^2} + 3 = 0\).
a) Phương trình \(7x + \dfrac{4}{7} = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số.
Khi đó, \(a = 7;b = \dfrac{4}{7}\).
b) \(\dfrac{3}{2}y - 5 = 4\)
\(\dfrac{3}{2}y - 5 - 4 = 0\)
\(\dfrac{3}{2}y - 9 = 0\)
Phương trình \(\dfrac{3}{2}y - 9 = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ay + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(y\) là ẩn số.
Khi đó, \(a = \dfrac{3}{2};b = - 9\)
c) Phương trình \(0t + 6 = 0\) không là phương trình bậc nhất một ẩn.
Mặc dù phương trình đã cho có dạng \(at + b = 0\) với \(a\) và \(b\) là các hệ số đã cho nhưng \(a = 0\).
d) Phương trình \({x^2} + 3 = 0\) không là phương trình bậc nhất một ẩn vì không có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số (do có \({x^2}\)).
Đúng 1
Bình luận (0)