Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua ba đỉnh A, B, C.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
a) Ta có: 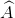 =
= 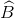 =
= 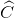 =
= 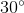 (gt)
(gt)
Suy ra:  =
= 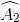 =
= 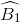 =
= 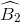 =
= 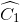 =
= 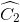 =
= 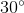 .
.
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của bà cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: 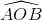 =
= 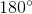 - (
- ( +
+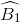 ) =
) = 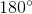 -
- 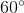 =
= 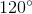
Tương tự ta suy ra 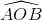 =
= 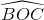 =
= 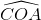 =
= 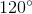 .
.
b) Từ 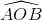 =
= 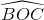 =
= 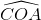 =
= 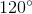 ta suy ra:
ta suy ra:
Cung ABC = BCA = CAB = 240º
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
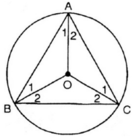
Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400
Cho đường tròn (O; R). Qua điểm A thuộc đường tròn, kẻ tiếp tuyến Ax, trên đó lấy điểm B sao cho \(OB=\sqrt{2}R\), OB cắt đường tròn (O) ở C.
a) Tính số đo góc ở tâm tạo bởi hai bán kính OA, OC;
b) Tính số đo các cung AC của đường tròn (O).
a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{AOC}=45^0\)
=>\(sđ\left(OA;OC\right)=45^0\)
b: Số đo cung AC nhỏ là:
\(sđ\stackrel\frown{AC}=45^0\)
Số đo cung AC lớn là:
3600-450=3150
cho đường tròn (O,R ) qua điểm A thuộc đường tròn , kẻ tiếp tuyến Ax trên đó lấy điểm B sao cho OB=căn hai R , OB cắt đường tròn (o) ở C a, tính sao đo góc ở tâm tạo bởi 2 bán kính OA, OC b, tính số đo các cung AC cửa đường tròn (O)
Bài 1: Cho đường tròn (O, R) và điểm M nằm ngoài đường tròn đó. Gọi MA, MB là hai tiếp tuyến với đường tròn tại A và B. Tính số đo của góc ở tâm tạo bởi hai bán kính OA và OB nếu:
a) ∠AMB = 70o
b) MA = R
c) MO = 2R
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc A M B = 35 o .
Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.
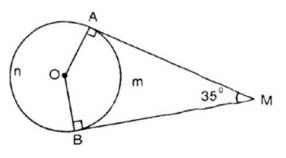
Góc ở tâm tạo bởi OA và OB là 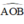
Tứ giác OAMB có:
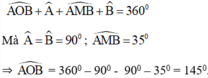
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh của hình nón là φ = 120 0 . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
![]()
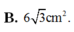
![]()
![]()
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R = 3 c m , góc ở đỉnh của hình nón là φ = 120 0. . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
A. 3 3 c m 2 .
B. 6 3 c m 2 .
C. 6 c m 2 .
D. 3 c m 2 .
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh hình nón là α = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2