Cho hình 88.
Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
Những câu hỏi liên quan
Cho hình 88.
a) Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
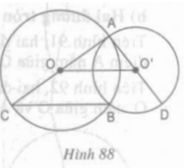
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Đúng 0
Bình luận (0)
Cho điểm M di động trên đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các hình vuông AMCD, BMEF.
a) Chứng minh rằng AE vuông góc với BC.
b) Gọi H là giao điểm của AE và BC. Chứng minh ba điểm D, H, F thẳng hàng.
c) Chứng minh rằng đường thẳng DF luôn đi qua một điểm cố định khi điểm M di động trên đoạn thẳng AB.
Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
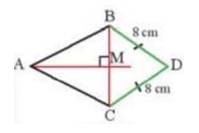
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B thuộc (O), C thuộc (O'). Đường thẳng BO cắt (O) tại điểm thứ hai là D.
a) Chứng minh rằng tứ giác CO'OB là một hình thang vuông.
b) Chứng minh rằng ba điểm A, C, D thẳng hàng.
c) Từ D kẻ tiếp tuyến DE với đường tròn (O') (E là tiếp điểm). Chứng minh rằng DB = DE.
Bài 4: (0,5 điểm) Cho đa thức Ax x 2x 4 4 2 . Chứng tỏ rằng Ax 0 với mọi x R . Bài 5: (3 điểm) Cho tam giác ABC vuông tại A có AB 5cm, BC 10cm. a) Tính độ dài AC. b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiếu của D trên BC. Chứng minh ΔABD ΔEBD và AE BD. c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh: ΔABC ΔAFC. d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng.
Đọc tiếp
Bài 4: (0,5 điểm) Cho đa thức Ax x 2x 4 4 2 . Chứng tỏ rằng Ax 0 với mọi x R . Bài 5: (3 điểm) Cho tam giác ABC vuông tại A có AB = 5cm, BC = 10cm. a) Tính độ dài AC. b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiếu của D trên BC. Chứng minh ΔABD = ΔEBD và AE BD. c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh: ΔABC = ΔAFC. d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng.
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Câu 1:Cho ΔABC vuông tại A, đường trung tuyến CM.a) Cho biết BC 10cm, AC 6cm. Tính độ dài đoạn thẳng AB, BM.b) Trên tia đối của tia MC lấy điểm D sao cho MD MC. Chứng minh rằng ΔMAC ΔMBD và AC BD.c) Chứng minh rằng AC + BC 2CM.d) Gọi K là điểm trên đoạn thẳng AM sao cho AM32AK. Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh rằng: CD 3IDCâu 2;Cho tam giác ABC vuông tại A có AB 5cm, BC 10cm.a) Tính độ dài AC.b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiế...
Đọc tiếp
Câu 1:Cho ΔABC vuông tại A, đường trung tuyến CM.a) Cho biết BC = 10cm, AC = 6cm. Tính độ dài đoạn thẳng AB, BM.b) Trên tia đối của tia MC lấy điểm D sao cho MD = MC. Chứng minh rằng ΔMAC = ΔMBD và AC = BD.c) Chứng minh rằng AC + BC > 2CM.d) Gọi K là điểm trên đoạn thẳng AM sao cho AM32AK=. Gọi N là giao điểm của CK và AD, I là giao điểm của BN và CD. Chứng minh rằng: CD = 3ID
Câu 2;Cho tam giác ABC vuông tại A có AB = 5cm, BC = 10cm.a) Tính độ dài AC.b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiếu của D trên BC. Chứng minh ΔABD = ΔEBD và BDAE⊥.c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh: ΔABC = ΔAFC.d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
BÀI 1: Cho tam giác ABC có D, E, F theo thứ tự là trung điểm của AB, AC, BC. Chứng minh BDEF là hình bình hành và suy ra BÀI 2: Cho hình bình hành ABCD (AB CD). Tia phân giác của góc A cắt BC tại I, tia phân giác góc C cắt AD tại K. Chứng minh: AICK là hình bình hành.BÀI 3: Cho tam giác ABC. Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB ở D.a) Chứng minh rằng tư giác ABDC là hình bình hành.b) Gọi M là trung điểm cạnh BC. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Đọc tiếp
BÀI 1: Cho tam giác ABC có D, E, F theo thứ tự là trung điểm của AB, AC, BC. Chứng minh BDEF là hình bình hành và suy ra
BÀI 2: Cho hình bình hành ABCD (AB < CD). Tia phân giác của góc A cắt BC tại I, tia phân giác góc C cắt AD tại K. Chứng minh: AICK là hình bình hành.
BÀI 3: Cho tam giác ABC. Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB ở D.
a) Chứng minh rằng tư giác ABDC là hình bình hành.
b) Gọi M là trung điểm cạnh BC. Chứng minh rằng ba điểm A, M, D thẳng hàng.