Tọa độ đỉnh của parabol (P): y = m 2 - 1 x 2 - 2 m + 1 x + 1 m ≠ ± 1 là
A. 2 m - 1 ; 1
B. - 2 m - 1 ; 9 m + 7 m - 1
C. 1 m - 1 ; 2 m - 1
D. 1 m - 1 ; 2 1 - m
Những câu hỏi liên quan
Cho hàm số parabol (P): y=x^2 và d(m)=mx-2
a) Vẽ B lên mặt phẳng tọa độ
b)Khi m=3 tìm tọa độ giao điểm của d(m) = d(3)
c) A ( xA,yA) B(xB,yB) là giao điểm của P và d(m). Tìm m để yA+yB=2(xA+xB)-1
trong mặt phẳng tọa độ oxy cho parabol (P):y=\(\frac{-x^2}{2}\)và đường thẳng d: y=3x+4
a, Tìm tọa độ giao điểm A,B của (P) và (d)
b,Tính độ dài AB
c,Tính diện tích tam giác OAB
omae wa mou shindeiru
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8 0. Tìm tọa độ điểm C. A. C( -1; 1) và C( 2 ; -3) B. C( 1;-1)và C( -2 ; 10) C. ( 1;-1) và C(2 ; -6) D. C( 1;1) và C( 2 ; -3)
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8= 0. Tìm tọa độ điểm C.
A. C( -1; 1) và C( 2 ; -3)
B. C( 1;-1)và C( -2 ; 10)
C. ( 1;-1) và C(2 ; -6)
D. C( 1;1) và C( 2 ; -3)
Đáp án B
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:
Vậy C( 1 ; -1) và C( -2 ; 10)
Đúng 0
Bình luận (0)
cho parabol (P) :y+x2 và đường thẳng (đ) có pt :y+2(m+1)x-3m+2
a) tìm tọa độ giao điểm của (P) va (d) với m=3
b) chứng minh rằng : (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A;B với mọi m
c) x1;x2 hoành độ của A;B.Tìm m để x1+x2 =20
Cho hai hàm số y x2/2 có đồ thị (P) và y -x + m có đồ thị (Dm).1. Với m 4, vẽ (P) và (D4) trên cùng một hệ trục tọa độ vuông góc Oxy. Xác định tọa độ các giao điểm của chúng.2. Xác định giá trị của m để:a) (Dm) cắt (P) tại điểm có hoành độ bằng 1.b) (Dm) cắt (P) tại 2 điểm phân biệt.c) (Dm) tiếp xúc (P). Xác định tọa độ tiếp điểm.
Đọc tiếp
Cho hai hàm số y = x2/2 có đồ thị (P) và y = -x + m có đồ thị (Dm).
1. Với m = 4, vẽ (P) và (D4) trên cùng một hệ trục tọa độ vuông góc Oxy. Xác định tọa độ các giao điểm của chúng.
2. Xác định giá trị của m để:
a) (Dm) cắt (P) tại điểm có hoành độ bằng 1.
b) (Dm) cắt (P) tại 2 điểm phân biệt.
c) (Dm) tiếp xúc (P). Xác định tọa độ tiếp điểm.
2:
a: Thay x=1 vào (P), ta được:
\(y=\dfrac{1^2}{2}=\dfrac{1}{2}\)
Thay x=1 và y=1/2 vào (D), ta được:
\(m-1=\dfrac{1}{2}\)
hay m=3/2
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2+x-m=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{1}{2}\cdot\left(-m\right)=2m+1\)
Để (D) cắt (P) tại hai điểm phân biệt thì 2m+1>0
hay m>-1/2
c: Để (D) tiếp xúc với (P) thì 2m+1=0
hay m=-1/2
Đúng 0
Bình luận (0)
Khi đường thẳng
∆
:
y
x
+
2
m
cắt parabol
P
:
y
x
2
-
x
+
3
tại hai điểm phân biệt A,B thì tọa độ trung điểm I của đoạn thẳng AB là A.
I
1
;
2
m
+
1
B.
I...
Đọc tiếp
Khi đường thẳng ∆ : y = x + 2 m cắt parabol P : y = x 2 - x + 3 tại hai điểm phân biệt A,B thì tọa độ trung điểm I của đoạn thẳng AB là
A. I 1 ; 2 m + 1
B. I - 1 ; 2 m - 1
C. I 2 ; 4 m + 2
D. I - 2 ; 4 m - 2
Phương trình hoành độ giao điểm của ∆ và (P) là
x 2 - x + 3 = x + 2 m ⇔ x 2 - 2 x + 3 = 0 (*)
Giả sử A ( x A ; y A ) thì B x B ; y B là các nghiệm của phương trình (*).
Theo định lí Vi-ét ta có x A + x B = 2 .
Ta có y A = x A + 2 m , y B = x B + 2 m nên y A + y B = x A + x B + 4 m = 2 + 4 m .
Tọa độ trung điểm I của đoạn thẳng AB là I x A + x B 2 ; y A + y B 2 = I 1 ; 2 m + 1 .
Chọn A.
Đúng 0
Bình luận (0)
Cho parabol (P) : y = x2 và đường thẳng d: y = x - m + 1
1. Tìm m để d tiếp xúc với (P). Khi đó tìm tọa độ tiếp điểm.
Tứ giác ABCD có tọa độ các đỉnh như sau : A(0 ; 2), B(3 ; 0), C(0 ; -2), D(-3 ; 0). Tứ giác ABCD là hình gì? Tính chu vi của tứ giác đó
Hình 2.6 cho biết đồ thị tọa độ – thời gian của một ôtô chuyển động thẳng, tốc độ của nó là 2 m/s. Tọa độ của ôtô lúc t 4s là A. 28 m. B. 20 m C. 15 m. D. 12 m
Đọc tiếp
Hình 2.6 cho biết đồ thị tọa độ – thời gian của một ôtô chuyển động thẳng, tốc độ của nó là 2 m/s. Tọa độ của ôtô lúc t = 4s là
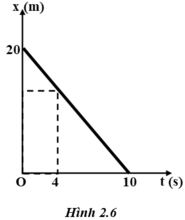
A. 28 m.
B. 20 m
C. 15 m.
D. 12 m
Chọn: D.
Tại thời điểm t = 0 thì x = x 0 = 20 m.
Vận tốc của ôtô là: v = - 20 10 = - 2 m / s
(vật chuyển động ngược chiều dương Ox).
=> Phương trình chuyển động của ôtô là: x = 20 - 2t
=> Tọa độ của ôtô lúc t = 4s là: x(4) = 12m.
Đúng 0
Bình luận (0)