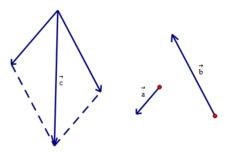
a →   ,   b →   ,   c →  đồng phẳng vì  a →  và  b → không cùng phương và có cặp số (2; -1) sao cho c →   =   2 a → -   b →

a) Đúng

b) Đúng

c) Sai

d) Đúng

TL: A, B, D: Đúng; C: Sai

Đáp án A

Điểm đầu là A: `\vec(AB), \vec(AC),\vec(AD),\vec(AE)`

Điểm đầu là B: `\vec(BA),\vec(BC),\vec(BD),\vec(BE)`.

Xíu nữa làm :v

1) Ta có:\(\overrightarrow{AB}+\overrightarrow{DE}-\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{AE}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{BE}+\overrightarrow{EC}\)

\(=\overrightarrow{AC}+\overrightarrow{BE}+\overrightarrow{CE}+\overrightarrow{EC}=\overrightarrow{AC}+\overrightarrow{BE}\left(đpcm\right)\)2) a) Ta có: \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)

\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\left(đpcm\right)\)

b) Ta có: \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)

\(=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\left(đpcm\right)\)c) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}-\overrightarrow{BD}\)

\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}\)

Ta có: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}+\overrightarrow{BC}\) ( đề bài bị lỗi gì à ?? :v ) hay do mình =))

b: \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)

Giả sử p ≠ 0 ta có:

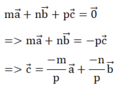
Do đó, ba vecto  a → ,   b → ,   c →  đồng phẳng theo định lí 1

Xét ΔABC có G là trọng tâm

nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

\(\dfrac{1}{3}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\)

\(=\dfrac{1}{3}\left(\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right)\)

\(=\dfrac{1}{3}\left(3\cdot\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)

\(=\dfrac{1}{3}\cdot3\cdot\overrightarrow{MG}=\overrightarrow{MG}\)