Tìm m để y = x 3 - 3 x 2 + m x - 1 có hai điểm cực trị tại x 1 , x 2 thỏa mãn x 1 2 + x 2 2 = 3
A. m = 3 2
B. m = 1
C. m = - 2
D. m = 1 2
tìm các giá trị thực của tham số m để đồ thị hàm số Cm : y= -x3 + 3mx2 - 2m3 có 2 điểm cực trị A, B sao cho đường thằng AB vuông góc với đường thằng d : y= -2x
trong mặt phẳng oxy : (d) y=(m+2)x+3 và (P) y=x^2 .tìm tất cả giá trị m để P và d cắt nhau tại 2 điểm phân biệt
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
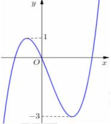
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Tìm tất cả các giá trị của tham số m để hàm số y = - x 3 + m x 2 - x có 2 điểm cực trị
A. | m | ≥ 2 3
B. | m | > 2
C. | m | > 3
D. | m | ≥ 3
Cho (P) y = x2 và (d) y = (2 + m) x + 3.
Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt và có hoành độ là các số nguyên
Cho hàm số y = x 3 − 3 m x + 1 1 . Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A
A. m=1/2
B. m=-3/2
C. m=-1/2
D. m=3/2
Đáp án A
Ta có y ' = 3 x 2 − 3 m = 3 x 2 − m
Hàm số có 2 điểm cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇒ m > 0 *
Khi đó B m ; 1 − 2 m m , C − m ; 1 + 2 m m ⇒ A B → = 2 − m ; 2 + 2 m m A B → = 2 + m ; 2 − 2 m m
Tam giác ABC cân tại A
⇒ A B = A C ⇔ 2 − m 2 + 2 + 2 m m 2 = 2 + m 2 + 2 − 2 m m 2
⇔ − 8 m + 16 m m = 0 ⇔ m 2 m − 1 = 0 ⇔ m = 0 m = 1 2
Kết hợp điều kiện * ⇒ m = 1 2
Tìm tất cả giá trị của m để hàm số y = 1/3.x3 – mx2 + (m2 – m + 1)x + 1 đạt cực đại tại x = 1
A. m = -2
B. m = -1
C. m = 2.
D. m = 1
Đáp án C
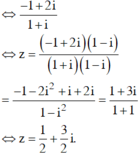
y’’ = 36x2 – 24x – 12
=> y’’(-1) = 48 > 0
Đồ thị hàm số có điểm cực tiểu là M(-1;-10) nên S = -11
Cho hàm số: y=(m-1)x+m (d)
a, Tìm m để hàm số đồng biến, nghịch biến
b, Tìm m để hàm số song song với trục hoành
c, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)
d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y=1
e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ \(x=2-\frac{\sqrt{3}}{2}\)
f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
1)Đồ thị hs y=\(\dfrac{2x-1}{x^2-x-1}\)có bao nhiêu đường tiệm cận?
2)Số tiệm cận của hs y=\(\dfrac{x^2-3x-1}{x^2-3x-4}\)
3)Tìm tất cả các giá trị của m để hs y=\(\dfrac{x^2+mx+1}{x+m}\) đạt cực trị tại x=2.
4)Để hs y=\(\dfrac{x^2+mx+1}{x-12}\) có cực đại,cực tiểu thì các giá trị của m là:
a)m=0 b)m thuộc R c)m<0 d)m>0