Giá trị của biểu thức T = i 2016 + i 216 + i 16 + i 6 + 1 ta có
A. 3
B. 4
C. 5
D. 6
Những câu hỏi liên quan
Cho các số phức
z
1
1
+
i
,
z
2
1
-
i
,
z
3
2
+
3
i
.
Giá trị của biểu thức
T
|
z
1
z
2...
Đọc tiếp
Cho các số phức z 1 = 1 + i , z 2 = 1 - i , z 3 = 2 + 3 i . Giá trị của biểu thức T = | z 1 z 2 + z 2 z 3 + z 3 z 1 | là
A. 6
B. 12
C. 6 2
D. 10
Cho các số phức
z
1
-
1
+
i
,
z
2
1
-
2
i
,
z
3
1
+
2
i
.
Giá trị của biểu thức
T
|
z
1
z...
Đọc tiếp
Cho các số phức z 1 = - 1 + i , z 2 = 1 - 2 i , z 3 = 1 + 2 i . Giá trị của biểu thức T = | z 1 z 2 + z 2 z 3 + z 3 z 1 | là
A. 1
B. 13
C. 5
D. 13
Cho các số phức
z
1
-
1
+
i
,
z
2
1
-
2
i
,
z
3
1
+
2
i
.
Giá trị của biểu thức
T
z
1...
Đọc tiếp
Cho các số phức z 1 = - 1 + i , z 2 = 1 - 2 i , z 3 = 1 + 2 i . Giá trị của biểu thức T = z 1 z 2 + z 2 z 3 + z 3 z 1 là
A. 1
B. 3
C. 4
D. 5
Giá trị của biểu thức đã cho tại x = 1
Giá trị của biểu thức đã cho tại x = 10
: Giá trị của biểu thức đã cho tại x = 1 phần 2
: Giá trị của biểu thức đã cho tại x = âm 3 phần 2
Giá trị của biểu thức đã cho tại x= -1
Biểu thức đâu hở bạn
Biểu thức đâu bạn
Đề đâu??????
Xem thêm câu trả lời
Các số thực x, y thỏa mãn: (x + 2y) + (2x - y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4
B. 5
C. 6
D. 7
Ta có: (x + 2y) + (2x - y)i = 6 + 7i
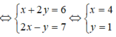
Vậy: T = 4 + 1 = 5
Chọn B
Đúng 0
Bình luận (0)
Cho biểu thức B=( x+3/ x -3 +2x2 - 6 /9 -x2 + x/x+3) :6x -12/2x2 -18
a, Tìm tập xác định và rút gọn biểu thức B
b, Tìm giá trị của B với | x +1|=2
c, Tìm giá trị nguyên của x để B nhận giá trị nguyên
\(B=\left(\dfrac{x+3}{x-3}+\dfrac{2x^2-6}{9-x^2}+\dfrac{x}{x+3}\right):\left(\dfrac{6x-12}{2x^2-18}\right)\) (1)
a ) ĐKXĐ : \(x\ne\pm3\)
\(\left(1\right)\Rightarrow B=\left(\dfrac{x+3}{x-3}+\dfrac{2x^2-6}{\left(x-3\right)\left(x+3\right)}+\dfrac{x}{x+3}\right):\left(\dfrac{6x-12}{2\left(x-3\right)\left(x+3\right)}\right)\)
\(\Leftrightarrow B=\left(\dfrac{x^2+6x+9-2x^2+6+x^2-3x}{\left(x-3\right)\left(x+3\right)}\right).\left(\dfrac{2\left(x-3\right)\left(x+3\right)}{6x-12}\right)\)
\(\Leftrightarrow B=\left(\dfrac{3x+15}{\left(x-3\right)\left(x+3\right)}\right)\left(\dfrac{2\left(x-3\right)\left(x+3\right)}{6x-12}\right)\)
\(\Leftrightarrow B=\dfrac{6x+30}{6x-12}\)
b ) \(\left|x+1\right|=2\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Khi x = 1 => \(B=\dfrac{6.1+30}{6.1-12}=-6\)
Khi \(x=-3\Rightarrow B=\dfrac{6.\left(-3\right)+30}{6.\left(-3\right)-12}=-\dfrac{2}{5}\)
c ) Ta có : \(B=\dfrac{6x+30}{6x-12}=\dfrac{6x-12+42}{6x-12}=1+\dfrac{42}{6x-12}\)
=> Để B nguyên thì \(42⋮6x-12\) \(\Rightarrow6x-12\inƯ\left(42\right)\)
Thay từng cái rồi tính .
Đúng 0
Bình luận (1)
cho biểu thức \(A=33×3+720:\left(x-6\right)\)
Tìm giá trị của x khi \(A=139\)
Tìm giá trị số tự nhiên của x để biểu thức A có giá trị lớn nhất, giá trị lớn nhất là bao nhiêu?
\(A=139\)
\(\Leftrightarrow720:\left(x-6\right)=40\)
\(\Leftrightarrow x-6=18\)
hay x=24
Đúng 0
Bình luận (1)
Câu hỏi : Tìm giá trị nhỏ nhất của biểu thức \(A=\)l x+\(\frac{1}{2}\)I + I x+\(\frac{1}{3}\)I + I x+\(\frac{1}{4}\)I
(Biết I I là giá trị tuyệt đối)_____Giúp mình nhé,các thành viên OLM!
Tìm x để biểu thức sau đạt giá trị lớn nhất. Hãy tìm giá trị lớn nhất đó.
A = 2026/ I x - 2013 I +2
TuanMinhAms sai rồi bn
để A lớn nhất \(\Rightarrow\left|x-2013\right|+2\) bé nhất
\(\left|x-2013\right|\ge0\Rightarrow\left|x-2013\right|+2\ge2\)
dấu "=" xảy ra khi \(\left|x-2013\right|=0\Rightarrow x=2013\)
khi đó GTLN của A = \(\frac{2026}{2}=1013\)
p/s: sai mk góp ý ko pk soi bài hay xúc phạm bn nha =]
Đúng 0
Bình luận (0)
\(A=\frac{2026}{\left|x-2013\right|+2}\)
\(Nx:\)\(\left|x-2013\right|\ge0\Rightarrow\left|x-2013\right|+2\ge2\)
A đạt giá trị lớn nhất khi và chỉ khi | x - 2013 | + 2 đạt giá trị nhỏ nhất
\(\left|x-2013\right|+2=2\Leftrightarrow\left|x-2013\right|=0\Leftrightarrow x=2013\)
\(\Rightarrow A_{Max}=\frac{2026}{2}=1013\Leftrightarrow x=2013\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức
A= -2x2-10y2-4xy+4x+4y+2016
A=−2x2−10y2+4xy+4x+4y+2016A=−2x2−10y2+4xy+4x+4y+2016
=−2.(x2+5y2−4xy−4x−4y)+2016=−2.(x2+5y2−4xy−4x−4y)+2016
=−2.(x2+4y2+4−4xy−4x+8y+y2−12y+36)+2.36+2016=−2.(x2+4y2+4−4xy−4x+8y+y2−12y+36)+2.36+2016
=−2.[(x−2y−2)2+(y−6)2]+2088=−2.[(x−2y−2)2+(y−6)2]+2088
Ta có: (x−2y−2)2+(y−6)2≥0(x−2y−2)2+(y−6)2≥0
⇒−2.[(x−2y−2)2+(y−6)2]≤0⇒−2.[(x−2y−2)2+(y−6)2]≤0
⇒−2.[(x−2y−2)2+(y−6)2]+2088≤2088⇒−2.[(x−2y−2)2+(y−6)2]+2088≤2088
⇒A≤2088⇒A≤2088
Vậy giá trị lớn nhất của A=2088A=2088 khi: \hept{x−2y−2=0y=6⇒\hept{x=2y+2y=6⇒\hept{x=14y=6\hept{x−2y−2=0y=6⇒\hept{x=2y+2y=6⇒\hept{x=14y=6
Thu gọn
Đúng 0
Bình luận (1)
\(A=-2\left(x^2+2xy+y^2\right)+4\left(x+y\right)-2-8y^2+2018\\ A=-2\left[\left(x+y\right)^2-2\left(x+y\right)+1\right]-8y^2+2018\\ A=-2\left(x+y-1\right)^2-8y^2+2018\le2018\\ A_{max}=2018\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Đúng 2
Bình luận (0)