Nêu định nghĩa tập hợp con của một tập hợp và định nghĩa hai tập hợp bằng nhau.

Những câu hỏi liên quan
Nêu định nghĩa tập hợp con của một tập hợp và định nghĩa hai tập hợp bằng nhau ?
Tập hợp con: Ta gọi A là tập hợp con của B, kí hiệu A⊂B, nếu mỗi phần tử của A là một phần tử của B
A⊂B ⇔ x ∈ A ⇒ x ∈B
Hai tập hợp bằng nhau: Hai tập hợp A và B là bằng nhau, kí hiệu A = B, nếu tất cả phần tử của chúng như nhau
A = B ⇔ A⊂B và B ⊂ A
Đúng 0
Bình luận (0)
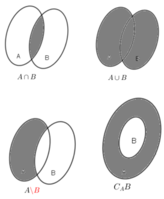
Nêu các định nghĩa hợp, giao, hiệu và phần bù của hai tập hợp. Minh họa các khái niệm đó bằng hình vẽ.
– Giao của hai tập hợp: A ∩ B = {x | x ∈ A và x ∈ B}
– Hợp của hai tập hợp: A ∪ B = {x | x ∈ A hoặc x ∈ B}
– Hiệu của A và B: A \ B = {x | x ∈ A và x ∉ B}
– Phần bù của B trong A: Nếu B ⊂ A thì A \ B gọi là phần bù của B trong A, kí hiệu: CAB.
- Hình minh họa:
Đúng 0
Bình luận (0)
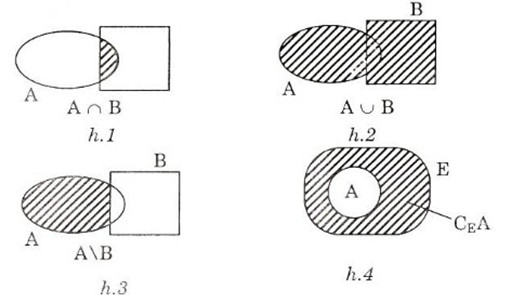
Nêu các định nghĩa hợp, giao, hiệu và phần bù của hai tập hợp. Minh họa các khái niệm bằng hình vẽ ?
A∩B ⇔ ∀x (x∈A và x∈B) (h.1)
A ∪B ⇔ ∀x (x∈A hoặc x∈B) (h.2)
A\B ⇔ ∀x (x∈A và x∉B) (h.3)
Cho A⊂E.CEA = {x/x∈E và x∉A} (h.4)
Đúng 0
Bình luận (0)
1.Cách kí hiệu tập hợp2.Tập hợp A là con của tập hợp B khi nào?Viết kí hiệu.Tập hợp A bằng tập hợp B khi nào?3.Viết tập hợp N;N*.Cho biết quan giữa 2 tập hợp trên4.Định nghĩa lũy thừa?phát biểu và viết dạng tổng quát của phép nhân;phép chia 2 lũy thừa cùng cơ số5.Nêu các tính chất chia hết của 1 tổng6.Nêu thứ tự thực hiện các phép tính trong biểu thức7.x thuộc ƯC(a,b,c) khi nào?x thuộc BC(a,b,c) khi nào?8.Thế nào là 2 số nguyên tố cùng nhau9.Cho biết mối quan hệ giữa các tập hợp N;N*;Z10.Tìm giá...
Đọc tiếp
1.Cách kí hiệu tập hợp
2.Tập hợp A là con của tập hợp B khi nào?Viết kí hiệu.Tập hợp A bằng tập hợp B khi nào?
3.Viết tập hợp N;N*.Cho biết quan giữa 2 tập hợp trên
4.Định nghĩa lũy thừa?phát biểu và viết dạng tổng quát của phép nhân;phép chia 2 lũy thừa cùng cơ số
5.Nêu các tính chất chia hết của 1 tổng
6.Nêu thứ tự thực hiện các phép tính trong biểu thức
7.x thuộc ƯC(a,b,c) khi nào?x thuộc BC(a,b,c) khi nào?
8.Thế nào là 2 số nguyên tố cùng nhau
9.Cho biết mối quan hệ giữa các tập hợp N;N*;Z
10.Tìm giá trị tuyệt đối của a;-a
Trong hai tập hợp A, B dưới đây, tập hợp nào là tập hợp con của tập còn lại? Hai tập hợp A và B có bằng nhau không?
A = {n ∈ N | n là một ước chung của 24 và 30}.
B = { n ∈ N | n là một ước của 6}.
A = {n ∈ N | n là một ước chung của 24 và 30} = {1; 2; 3; 6}.
B = {n ∈ N | n là một ước của 6} = {1; 2; 3; 6}.
Ta thấy A ⊂ B và B ⊂ A nên A = B.
Đúng 0
Bình luận (0)
Cho tập hợp X = {0;1;2;...;14}. Gọi A là một tập hợp gồm 6 phần tử được lấy ra từ X. Chứng minh rằng trong các tập hợp con thực sự của A luôn tìm được hai tập có tổng các phần tử bằng nhau. (Tập hợp con thực sự của tập Y là tập hợp con của Y khác tập rỗng và khác Y)
Vì tập hợp A gồm 6 phần tử nên có: 26-1=63 tập con (khác rỗng)
Tập con có giá trị lớn nhất là:
9+10+11+12+13+14=69
Các tập còn lại không vượt quá:
10+11+12+13+14=60
Như vậy có 61 giá trị của tập con A
Mà có 63 tập nên có 32 tập có giá trị bằng nhau
-khong chac nha
Trong hai tập hợp A, B dưới đây, tập hợp nào là tập hợp con của tập còn lại? Hai tập hợp A và B có bằng nhau không?
A là tập hợp các hình vuông;
B là tập hợp các hình thoi.
Vì mỗi hình vuông đều là một hình thoi nên A ⊂ B.
Có những hình thoi không phải là hình vuông nên B ⊄ A.
Vậy A ≠ B.
Đúng 0
Bình luận (0)
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
Đọc tiếp
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
giải gấp cho mình mình đang vộiCâu 1: Điền vào chỗ chấm.a) Tập hợp A gồm các số tự nhiên x mà 50x có phần tử vì................b) Tập hợp B gồm các số tự nhiên x mà 23x có phần tử vì.................c) Tập hợp C gồm các số tự nhiên x mà 00x có phần tử vì.................Số phần tửcủa tập hợpTẬP HỢPTập hợpconCó vô số phần tửCó nhiều phần tửCó một phần tửKhông có phần tử nàoTập số tự nhiênNếu mọi phần tử của tập hợp A đềuthuộc tập hợp B thì A là tập con của B.ABNếu ,ABBA thì ABKí hiệuĐịn...
Đọc tiếp
giải gấp cho mình mình đang vội
Câu 1: Điền vào chỗ chấm.
a) Tập hợp A gồm các số tự nhiên x mà 50x có phần tử vì
................
b) Tập hợp B gồm các số tự nhiên x mà 23x có phần tử vì
.................
c) Tập hợp C gồm các số tự nhiên x mà 00x có phần tử vì
.................
Số phần tử
của tập hợp
TẬP HỢP
Tập hợp
con
Có vô số phần tử
Có nhiều phần tử
Có một phần tử
Không có phần tử nào
Tập số tự nhiên
Nếu mọi phần tử của tập hợp A đều
thuộc tập hợp B thì A là tập con của B.
AB
Nếu ,ABBA thì AB
Kí hiệu
Định nghĩa
Hai tập hợp
bằng nhau
Tập rỗng
d) Tập hợp D gồm các số tự nhiên x mà 00x có phần tử vì
.................
e) Tập hợp E gồm các số tự nhiên x mà 03x có phần tử vì
.................












