A∩B ⇔ ∀x (x∈A và x∈B) (h.1)
A ∪B ⇔ ∀x (x∈A hoặc x∈B) (h.2)
A\B ⇔ ∀x (x∈A và x∉B) (h.3)
Cho A⊂E.CEA = {x/x∈E và x∉A} (h.4)
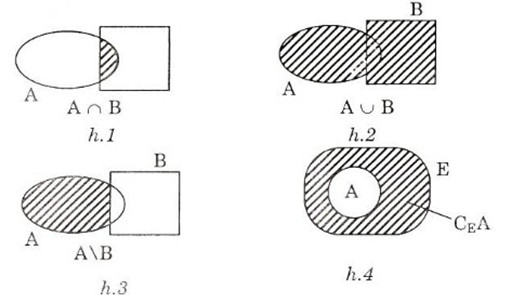
A∩B ⇔ ∀x (x∈A và x∈B) (h.1)
A ∪B ⇔ ∀x (x∈A hoặc x∈B) (h.2)
A\B ⇔ ∀x (x∈A và x∉B) (h.3)
Cho A⊂E.CEA = {x/x∈E và x∉A} (h.4)

Nêu định nghĩa tập hợp con của một tập hợp và định nghĩa hai tập hợp bằng nhau ?
Xét mối quan hệ bao hàm giữa các tập hợp sau :
A là tập hợp các hình tứ giác
B là tập hợp các hình bình hành
C là tập hợp các hình thang
D là tập hợp các hình chữ nhật
E là tập hợp các hình vuông
G là tập hợp các hình thoi
Bài1 : Cho A = {0;1;2;3;4;5;6;9} ; B = {0;2;4;6;8;9}, C= {3;4;5;6;7}
a. Tìm 𝐴 ∩ 𝐵; 𝐴 \ 𝐵
b. So sánh hai tập : A∩(B\C)và (A∩B)\C
Bài 2 : Tìm tất cả các tập hợp X thỏa mãn : 𝑋 ⊂ 𝐴; 𝑋 ⊂ 𝐵 với 𝐴= {1;2;3;4}; 𝐵= {0;2;4;6;8}
Bài 3 : Xác định các tập hợp : 𝐴 ∪ 𝐵; 𝐴 ∩ 𝐵; 𝐴 \ 𝐵; 𝐵 \ 𝐴 và biểu diễn chúng trên trục số ?
a. 𝐴= [−4;4] ; B=[1;7]
b. 𝐴= (−∞;−2] , B= [3;+∞)
1.viết tập hợp các số tự nhiên lẻ bé thua 25 bằng 2 cách.
2.cho tập hợp A=0;1;2;3;...............2018
a, tính số phần tử của A
b, gọi S là tổng các phần tử của A .tính S
3. chứng minh rằng nếu A là tập hợp con của B và B là tập hợp con của D thì A là tập hợp con của D
4. hãy xác định tập hợp sau = cách chỉ ra tính chất đặc trưng của các phần tử của nó.
a, tập hợp M các số tự nhiên chia hết cho 5 và bé thua 30
b,tập hợp P các số : 1;4;9;16;25;36;49;64;81
Nêu định nghĩa đoạn \(\left[a;b\right]\), khoảng \(\left(a;b\right)\), nửa khoảng [a;b), (a,b], (\(-\infty;b\)], [a; \(+\infty\)).
Viết tập hợp R các số thực dưới dạng 1 khoảng ?
Cho các tập hợp A= {x ∈ R\(|\)-3<x<3}; B= {x ∈ R\(|\)-1 ≤ x ≤ 5}; C = {x ∈ R\(|\)Ixl ≥ 2}. Xác định các tập hợp A\(\cap\)B\(\cap\)C
A. [2;3)
B. (2;3)
C. [-1;3)
D. R
Cho 2 tập hợp: A={x € Z| -2<x<2} , B={0,1,2,3,4,5}
Xác định: A giao B, A hợp B
cho tập hợp A={ x∈R / \(^{x^2+3x+4=0}\)}, tập hợp nào sau đây la đúng? Giải thích vì sao?
a) tập hợp A có một phần tử
b) tập hợp A có hai phần tử
c) tập hợp A=∅
d) tập hợp A có vô số phần tử
Cho A, B là hai tập hợp và mệnh đề P : "A là một tập hợp con của B"
a) Viết P dưới dạng một mệnh đề kéo theo
b) Lập mệnh đề đảo của P
c) Lập mệnh đề phủ định của P và viết nó dưới dạng một mệnh đề kéo theo