Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:
M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị cực tiểu.
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho :
\(MA^2+MB^2+MC^2+MD^2\) đạt giá trị cực tiểu
Trong không gian hệ tọa độ Oxyz, cho tứ diện ABCD với A(2;3;2), B(6;-1;-2), C(-1;-4;3), D(6;-1;-2). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất.
A. M(1;1;0)
B. M(0;1;-1)
C. M(1;1;-1)
D. M(-1;1;-1)
Đáp án B.
Ta có:
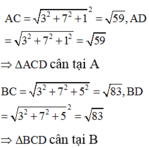
Từ đó gọi M là trung điểm của CD ta có ![]()
Do đó chu vi ∆ A B M là
![]()
(vì AB không thay đổi), tức là khi M là trung điểm cuả CD hay M(0;1;-1)
Cho tứ giác ABCD và một điểm M nằm trong tứ giác đó. Tìm vị trí của điểm M sao cho: MA + MB + MC + MD đạt giá trị nhỏ nhất.
Gọi I là giao điểm
Lấy điểm M bất kì trong tứ giác ABCD
Ta có: \(MA+MC\ge AC\)
\(MB+MD\ge BD\)
nên \(MA+MB+MC+MD\ge AC+BD\)( có giá trị không đổi )
Để MA + MB + MC + MD đạt giá trị nhỏ nhất thì:
\(MA+MB+MC+MD=AC+BD\Leftrightarrow"="MA+MC\ge AC\)\(\Rightarrow M\in AC\)
Tương tự xảy ra \("="\Leftrightarrow MB+MD\ge BD\Rightarrow M\in BD\)
Nên M trùng O
Vậy......................
ta có AM+MC> AC(bđt tam giác)
(dấu = xảy ra khi M thuộc AC) (1)
ta lại có BM+MD> BD (bđt tam giác)
(dấu = xảy ra khi M thuộc BD) (2)
lấy (1)+(2) suy ra: AM+MC+BM+MD> AC+BD
và đạt giá trị nhỏ nhất khi :AM+MC+BM+MD=AC+BD
vậy M nằm ở giao điểm AC và BD
Hoặc
MA+MB+MC+MD
(MA+MD)+(MB+MC)
(MA+MD) nhỏ nhất khi AMD trên đường thẳng
(MB+MC) nhỏ nhất khi BMC trên đường thẳng
\(\Rightarrow\) GTNN đạt được khi M là giao hai đường chéo AD và BC
Vậy..................................
Trong không gian hệ tọa độ Oxyzcho tứ diện ABCD với A(2;3; 2), B(6;-1;-2), C(-l;-4;3),D(l;6;-5). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất
A. M(1;1;0)
B. M(0;1;-1)
C. M(1;1;-1)
D. M(-1;1;-1)
Trong không gian với hệ tọa độ Oxya, cho tứ diện ABCD có A(-1;1;6), B(-3;-2;-4), C(1;2;-1), D(2;-2;0). Điểm M(a,b,c) thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất. Tính a+b+c.
A.1.
B.2.
C.3.
D.0.
Cho hcn ABCD. Lấy M thuộc tia đối của tia DC, lấy N thuộc DC sao cho góc MAN=90 độ
a)C/m già trị của tổng 1/AM^2 + 1/AN^2 không thuộc vị trí của M và N
b)Tìm vị trí của M và N để diện tích AMN nhỏ nhất
cho tứ giác ABCD. Xác định vị trí của điểm M nằm trong tứ giác ABCD sao cho tổng MA +MB + MC + MD đạt giá trị nhỏ nhất
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất
2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất
3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ \(IH⊥BC,IK⊥AC,IL⊥AB\). Xác định vị trí của I để \(AL^2+BH^2+CK^2\) nhỏ nhất
4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất
Cho hình vuông ABCD. Điểm M thuộc cạnh AB(M khác A và B). Tia CM cắt tia DA tại N. Vẽ Cx vuông góc với CM và cắt tia AB tại E. Gọi H là trung điểm của đoạn NE. Tìm vị trí của điểm M trên cạnh AB để diện tích tứ giác NACE bằng 15/8 diện tích hình vuông ABCD.
Mk chỉ nêu cách làm bạn tự triển khai nha!
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)