Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: d ' : x - 1 3 = y - 5 2 = z - 4 2
Những câu hỏi liên quan
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau:
d
:
x
t
y
1
+
t
z
2
-...
Đọc tiếp
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: d : x = t y = 1 + t z = 2 - t và d ' : x = 9 + 2 t ' y = 8 + 2 t ' z = 10 - 2 t '
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau:
d
:
x
+
1
1
y
-
1
2
z
+...
Đọc tiếp
Xét vị trí tương đối của các cặp đường thẳng d và d’ cho bởi các phương trình sau: d : x + 1 1 = y - 1 2 = z + 3 3
Xét vị trí tương đối các cặp đường thẳng d và d cho bởi các phương trình sau:
a
)
d
:
x
-
3
+
2
t
y
-
2
+...
Đọc tiếp
Xét vị trí tương đối các cặp đường thẳng d và d' cho bởi các phương trình sau: a ) d : x = - 3 + 2 t y = - 2 + 3 t z = 6 + 4 t d ' : x = 5 + t ' y = - 1 - 4 t ' z = 20 + t '
b ) d : x = 1 + t y = 2 + t z = 3 - t d ' : x = 1 + 2 t ' y = - 1 + 2 t z = 2 - 2 t '
Xét vị trí tương đối của các cặp đường thẳng d và d cho bởi các phương trình sau :
a) d:left{{}begin{matrix}x-3+2ty-2+3tz6+4tend{matrix}right. và d:left{{}begin{matrix}x5+ty-1-4tz20+tend{matrix}right.
b) d:left{{}begin{matrix}x1+ty2+tz3-tend{matrix}right. và d:left{{}begin{matrix}x1+2ty-1+2tz2-2tend{matrix}right.
Đọc tiếp
Xét vị trí tương đối của các cặp đường thẳng d và d' cho bởi các phương trình sau :
a) \(d:\left\{{}\begin{matrix}x=-3+2t\\y=-2+3t\\z=6+4t\end{matrix}\right.\) và \(d':\left\{{}\begin{matrix}x=5+t'\\y=-1-4t'\\z=20+t'\end{matrix}\right.\)
b) \(d:\left\{{}\begin{matrix}x=1+t\\y=2+t\\z=3-t\end{matrix}\right.\) và \(d':\left\{{}\begin{matrix}x=1+2t'\\y=-1+2t'\\z=2-2t'\end{matrix}\right.\)
a) Đường thẳng d đi qua M1( -3 ; -2 ; 6) và có vectơ chỉ phương (2 ; 3 ; 4).
Đường thẳng d' đi qua M2( 5 ; -1 ; 20) và có vectơ chỉ phương (1 ; -4 ; 1).
Ta có = (19 ; 2 ; -11) ;
= (8 ; 1 ; 14)
và = (19.8 + 2 - 11.4) = 0
nên d và d' cắt nhau.
Nhận xét : Ta nhận thấy ,
không cùng phương nên d và d' chỉ có thể cắt nhau hoặc chéo nhau.
Xét hệ phương trình:
Từ (1) với (3), trừ vế với vế ta có 2t = 6 => t = -3, thay vào (1) có t' = -2, từ đó d và d' có điểm chung duy nhất M(3 ; 7 ; 18). Do đó d và d' cắt nhau.
b) Ta có : (1 ; 1 ; -1) là vectơ chỉ phương của d và
(2 ; 2 ; -2) là vectơ chỉ phương của d' .
Ta thấy và
cùng phương nên d và d' chỉ có thể song song hoặc trùng nhau.
Lấy điểm M(1 ; 2 ; 3) ∈ d ta thấy M d' nên d và d' song song.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 2 ): x − 2y + z + 3 = 0, ( α ' 2 ): x − 2y – z + 3 = 0
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 3 ): x – y + 2z – 4 = 0, ( α ' 3 ): 10x − 10y + 20z – 40 = 0
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 1 ): 3x − 2y − 3z + 5 = 0, ( α ' 1 ): 9x − 6y − 9z – 5 = 0
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
t
y
1
+
2
t...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = t y = 1 + 2 t z = 1 - t và ( α ): x + 2y + z - 3 = 0
Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng ( α ) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0
⇔ 4t = 0 ⇔ t = 0
Vậy đường thẳng d cắt mặt phẳng ( α ) tại M 0 (0; 1; 1)
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp đường thẳng d1 và d2 sau đây:
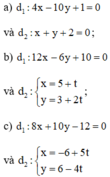
Cách 1: Dựa vào số nghiệm của hệ phương trình:
a) Xét hệ phương trình
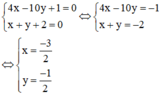
Hệ phương trình có nghiệm duy nhất nên (d1) cắt (d2).
b) Xét hệ phương trình
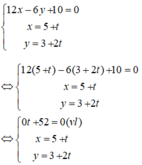
Hệ phương trình trên vô nghiệm nên hai đường thẳng trên song song.
c) Xét hệ phương trình
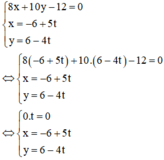
Hệ phương trình trên có vô số nghiệm nên hai đường thẳng trùng nhau.
Cách 2: Dựa vào vị trí tương đối của các vectơ chỉ phương (hoặc vectơ pháp tuyến).
a) d1 nhận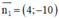 
là một vectơ pháp tuyến
d2 nhận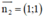 
là 1 vtpt
Nhận thấy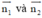 
không cùng phương nên d1 cắt d2.
b) d1 nhận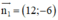 
là 1 vtpt ⇒ d1 nhận 
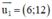là 1 vtcp
d2 nhận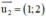 
là 1 vtcp.
Nhận thấy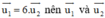 
cùng phương
⇒ d1 và d2 song song hoặc trùng nhau.
Xét điểm M(5;3) có:
M(5; 3) ∈ d2
12.5 – 6.3 + 10 = 52 ≠ 0 nên M(5; 3) ∉ d1.
Vậy d1 và d2 song song.
c) d1 nhận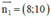 
là 1 vtpt ⇒ d1 nhận 
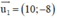là 1 vtcp.
d2 nhận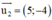 
là 1 vtcp.
Nhận thấy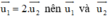 
cùng phương
⇒ d1 và d2 song song hoặc trùng nhau.
Xét M(–6; 6) ∈ d2; M(–6; 6) ∈ d1 (Vì 8.(–6) + 10.6 – 12 = 0)
⇒ d1 và d2 trùng nhau.
Đúng 0
Bình luận (0)