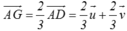Hãy phân tích các vectơ a→, b→ theo hai vectơ i→ và j→ trong hình (h.1.23)
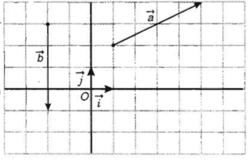
Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
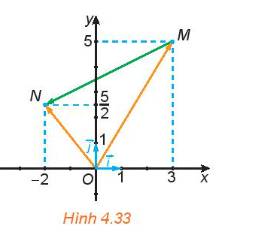
Tham khảo:
Dựng hình bình hành OAMB và OCND như hình dưới:
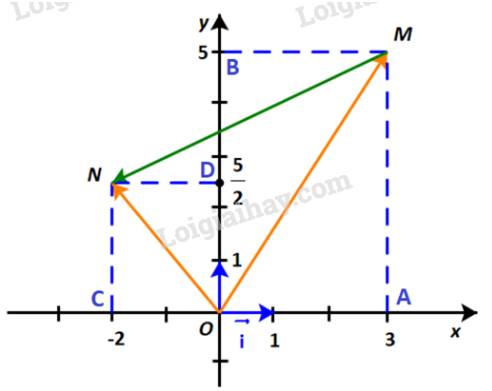
Khi đó: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) và \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} \).
Dễ thấy:
\(\overrightarrow {OA} = 3\;\overrightarrow i ;\;\,\overrightarrow {OB} = 5\;\overrightarrow j \) và \(\overrightarrow {OC} = - 2\;\overrightarrow i ;\;\,\overrightarrow {OD} = \frac{5}{2}\;\overrightarrow j \)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {OM} = 3\;\overrightarrow i + 5\;\overrightarrow j \\\overrightarrow {ON} = - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j \end{array} \right.\)
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \) (quy tắc hiệu)
\(\begin{array}{l} \Rightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j } \right) - \left( {\;3\;\overrightarrow i + 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i - 3\;\overrightarrow i } \right) + \left( {\frac{5}{2}\;\overrightarrow j - 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \end{array}\)
Vậy \(\overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \).
Cho vectơ a = (2; -2), vectơ b = (1; 4). Hãy phân tích vectơ c (5; 0) theo hai vectơ a và b.
Cho các vectơ a → = 4 ; - 2 ; b → = - 1 ; - 1 ; c → = 2 ; 5 . Phân tích vectơ b → theo hai vectơ a → và c → , ta được:
A. b → = - 1 8 a → - 1 4 c →
B. b → = 1 8 a → - 1 4 c →
C. b → = - 1 2 a → - 4 c →
D. b → = - 1 8 a → + 1 4 c →
Cho các vectơ a → = 4 ; - 2 , b → = - 1 ; - 1 , c → = 2 ; 5 . Phân tích vecto b → theo hai vectơ a → và c → ta được:
![]()
![]()
![]()
![]()
Cho tam giác ABC . Gọi D là điểm sao cho B D → = 2 3 B C → và I là trung điểm của cạnh AD , M là điểm thỏa mãn A M → = 2 5 A C → Vectơ B I → được phân tích theo hai vectơ B A → v à B C → .Hãy chọn khẳng định đúng trong các khẳng định sau?
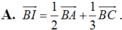
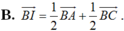
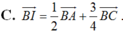
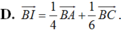
Chọn A.
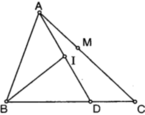
Ta có: I là trung điểm của cạnh AD nên

Cho hình thang OABC có M, N lần lượt là trung điểm của OB và OC
a. Phân tích vectơ \(\overrightarrow{AM}\) theo \(\overrightarrow{OA}\) và\(\overrightarrow{OB}\)
b. Phân tích các vectơ \(\overrightarrow{BN}\) , \(\overrightarrow{MN}\) theo 2 vectơ \(\overrightarrow{OB}\) và\(\overrightarrow{OC}\)
a.
Do M là trung điểm OB \(\Rightarrow\overrightarrow{OM}=\dfrac{1}{2}\overrightarrow{OB}\)
\(\Rightarrow\overrightarrow{AM}=\overrightarrow{AO}+\overrightarrow{OM}=-\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}\)
b.
Do N là trung điểm OC \(\Rightarrow\overrightarrow{ON}=\dfrac{1}{2}\overrightarrow{OC}\)
\(\Rightarrow\overrightarrow{BN}=\overrightarrow{BO}+\overrightarrow{ON}=-\overrightarrow{OB}+\dfrac{1}{2}\overrightarrow{OC}\)
\(\overrightarrow{MN}=\overrightarrow{MO}+\overrightarrow{ON}=-\overrightarrow{OM}+\overrightarrow{ON}=-\dfrac{1}{2}\overrightarrow{OB}+\dfrac{1}{2}\overrightarrow{OC}\)
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt u → = A E → ; v → = A F → . Hãy phân tích các vectơ theo hai vectơ u → , v →
A. ![]()
B. ![]()
C. ![]()
D. tất cả sai
Trong mặt phẳng tọa độ,cho vectơ u=1/2 vectơ i -5 vectơ j và vectơ v=K vectơ i -4 vectơ j a)tìm các giá trị của K để | vectơ u|=| vectơ v| Giúp tui với mng
Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt u → = A E → ; v → = A F → Hãy phân tích các vectơ A G → theo hai vectơ u → ; v →
A. A G → = 2 u → + 2 v →
B. A G → = 3 u → + 3 v →
C. A G → = 2 3 u → + 2 3 v →
D. tất cả sai
Chọn C.
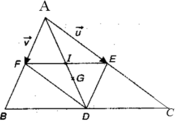
+ Ta có ![]() ( quy tắc hình bình hành)
( quy tắc hình bình hành)
Do đó: