Một vật dao động điều hoà quanh vị trí cân bằng theo phương trình x = 4cos(πt+π/2) (cm); t tính bằng giây. Biết rằng cứ sau những khoảng thời gian π/40 (s) thì động năng lại bằng nửa cơ năng. Tại những thời điểm nào thì vật có vận tốc bằng không?
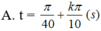
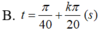
![]()

Chất điểm có khối lượng m1 = 50 gam dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động x1 = sin(5πt + π/6) (cm). Chất điểm có khối lượng m2 = 100 gam dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động x2 = 5sin(πt – π/6)(cm). Tỉ số cơ năng trong quá trình dao động điều hoà của chất điểm m1 so với chất điểm m2 bằng:
A. 1/2.
B. 2.
C. 1.
D. 1/5.
Một vật thực hiện dao động điều hòa xung quanh vị trí cân bằng theo phương trình x = 4cos(4πt – 0,5π) cm. Chu kì dao động của vật là
A. 2 s.
B. 0,5π s.
C. 2π s.
D. 0,5 s
ü Đáp án D
+ Chu kì dao động của vật
T = 2 π ω = 0 , 5 s
Một vật thực hiện dao động điều hòa xung quanh vị trí cân bằng theo phương trình x = 4cos(4πt – 0,5π) cm. Chu kì dao động của vật là
A. 2 s.
B. 0,5π s.
C. 2π s.
D. 0,5 s.
Một chất điểm dao động điều hòa theo phương trình x=4cos(πt-π/3) cm (t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = −2 cm lần thứ 2019 tại thời điểm
A. 2019 s
B. 4018 s
C. 2018 s
D. 4037 s
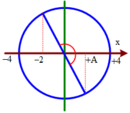
Biểu diễn dao động tương ứng trên đường tròn
Tại t = 0, chất điểm đi qua vị trí x=A/2=2cm theo chiều dương
Trong mỗi chu kì chất điểm đi qua vị trí x = -2 hai lần
Ta tách: 2019 = 2018 + 1 → 2018 lần ứng với 1009T
→ Tổng thời gian t=1009T+T/2=2019s
Chọn đáp án A
Chất điểm có khối lượng m1 = 500gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 1 = cos ( 5 πt + π / 6 ) (cm). Chất điểm có khối lượng m2 = 100 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 2 = 5 cos ( πt - π / 6 ) (cm). Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m1 so với m2 bằng
A. 1/2.
B. 2.
C. 5.
D. 1/5.
Một vật nhỏ dao động điều hòa dọc theo trục Ox (vị trí cân bằng ở O) với biên độ 4 cm và tần số 10 Hz. Tại thời điểm t = 0, vật có li độ 4 cm. Phương trình dao động của vật là A.x = 4cos(20 π t + π ) cm. B.x = 4cos20 π t cm. C.x = 4cos(20 π t – 0,5 π ) cm. D.x = 4cos(20 π t + 0,5 π ) cm.
Chất điểm có khối lượng m 1 = 50 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 1 = sin ( 5 πt + π / 6 ) (cm). Chất điểm có khối lượng m 2 = 100 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 2 = 5 sin ( πt - π / 6 ) (cm). Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m 1 so với chất điểm m 2 bằng
A. 1/2
B. 2
C. 1
D. 1/5
Một con lắc lò xo nằm ngang dao động điều hoà xung quanh vị trí cân bằng với chu kỳ T = π/10 s. Đặt trục tọa độ Ox nằm ngang, gốc O tại vị trí cân bằng. Cho rằng lúc t = 0, vật ở vị trí có li độ x = -1 cm và được truyền vận tốc 20√3 cm/s theo chiều dương. Khi đó phương trình dao động của vật có dạng:
A. x = 2 sin (20t + π/6) cm.
B. x = 2 cos (20t - π/6) cm.
C. x = 2 sin (20t - π/6) cm.
D. x = 2 sin (20t - π/3) cm.
Chọn C
+ ω = 2π : T = 20 rad/s.
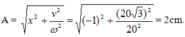
+ t = 0: x = 2cosφ = -1 => 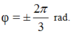
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
Bài 2: Một vật dao động điều hoà với phương trình x = 4cos(4πt + π/6) cm. Tìm số lần vật qua vị trí x = 2cm theo chiều dương trong thời gian 5,75s tính từ thời điểm gốc.
ω=4π=>T=0,5s
\(\dfrac{t}{T}=\dfrac{5,75}{0,5}=11+0,5\)
tdư=0,5T=>α=π
khi t=0 có x0=2\(\sqrt{3}\) cm
Vẽ đường tròn thấy trong khoảng thời gian 0,5T vật không đi qua vị trí x=2 cm theo chiều dương lần nào cả
=> số lần vật đi qua vị trí x=2cm theo chiều dương trong 5,75s là 11 lần