Cho α là góc nhọn bất kỳ. Khi đó C = sin4 + cos4 bằng:
A. C = 1 - 2 sin 2 α . c o s 2
B. C = 1
C. C = sin 2 α . c o s 2
D. C = 1 + 2 sin 2 α . c o s 2
Cho α là góc nhọn bất kỳ. Khi đó C = sin 6 α + cos 6 α + 3 sin 2 α . cos 2 α bằng:
A. C = 1 - 3 sin 2 α . cos 2 α
B. C = 1
C. C = sin 2 α . cos 2 α
D. C = 3 sin 2 α . cos 2 α - 1
Ta có:

= sin 6 α + cos 6 α + 3 sin 2 α . cos 2 α . ( sin 2 α + cos 2 α ) v ì sin 2 α + cos 2 α = 1
= ( sin 2 α ) 3 + 3 sin 2 α 2 cos 2 + 3 sin 2 α . cos 2 α 2 + cos 2 α 3

Đáp án cần chọn là: B
Cho góc α thỏa mãn tanα = 5. Tính P= sin4 α - cos4 α
A. P = 2
B. P = 1/2
C. P = 11/13
D. P = 12/13
Chọn D.
Ta có P = ( sin2α - cos2α) ( sin2α + cos2α) = sin2α - cos2α (*)
Chia hai vế của (*) cho cos2 α ta được ![]()
Tương đương: P(1 + tan2α) = tan2α - 1
![]()
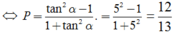
Bài 1.
Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các góc A, B, C.
a, Cmr a / sin A = b / sin B = c / sin C
b, Có thể xảy ra đẳng thức sin A = sin B + sin C không ? Vì sao?
Bài 2.
Cho tam giác ABC có góc nhọn B = α.
a, Biết cos α = 0,4, hãy tính sin α, tan α, cotg α.
b, Biết cos α - sin α = 1/5. Tính cotg α.
Giúp e với nak, càng nhanh càng tốt. E cảm ơn nhìu ![]()
Bài 2:
a: \(\sin\alpha=\sqrt{1-\left(\dfrac{2}{5}\right)^2}=\dfrac{\sqrt{21}}{5}\)
\(\tan\alpha=\dfrac{\sqrt{21}}{5}:\dfrac{2}{5}=\dfrac{\sqrt{21}}{2}\)
\(\cot\alpha=\dfrac{2}{\sqrt{21}}=\dfrac{2\sqrt{21}}{21}\)
b: Đặt \(\cos\alpha=a;\sin\alpha=b\)
Theo đề, ta có: a-b=1/5
=>a=b+1/5
Ta có: \(a^2+b^2=1\)
\(\Leftrightarrow b^2+\dfrac{2}{5}b+\dfrac{1}{25}+b^2-1=0\)
\(\Leftrightarrow2b^2+\dfrac{2}{5}b-\dfrac{24}{25}=0\)
\(\Leftrightarrow10b^2+2b-24=0\)
=>b=4/5
=>a=3/5
\(\cot\alpha=\dfrac{a}{b}=\dfrac{3}{4}\)
Cho α là góc nhọn bất kỳ. Biểu thức Q = 1 + sin 2 α 1 − sin 2 α bằng:
A. Q = 1 + tan 2 α
B. Q = 1 + 2 tan 2 α
C. Q= 1 - tan 2 α
D. Q = 2 tan 2 α
![]()
Q = 1 + sin 2 α 1 − sin 2 α = 1 − sin 2 α + 2 sin 2 α 1 − sin 2 α = 1 − sin 2 α 1 − sin 2 α + 2 sin 2 α cos 2 α
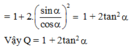
Đáp án cần chọn là: B
Chứng minh rằng:
a) sin4 α + sin2 α.cos2 α + cos2α = 1
b) (1+tan α).(1+cot α).sin α.cos α=1 + 2.sin α.cos α
c) sin6 α+cos6 α + 3 sin2 α.cos2 α = 1
a: \(=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1^2=1\)
Cho α là góc nhọn bất kỳ. Biểu thức Q = cos 2 α − sin 2 α c o s α . sin α bằng:
A. Q = cot α − tan α
B. Q = cot α + tan α
C. Q = tan α − cot α
D. Q = 2 tan α
Với tan α = sin α cos α ; cot α = cos α sin α ta có:
Q = Q = cos 2 α − sin 2 α c o s α . sin α = cos 2 α sin α . cos α − sin 2 α sin α . cos α = cos α sin α − sin α cos α
= cot α − tan α
Vậy Q = cot α − tan α
Đáp án cần chọn là: A
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Câu 50**: Cho góc nhọn α tuỳ ý giá trị biểu thức \(\dfrac{tan\alpha}{cot\alpha}+\dfrac{cot\alpha}{tan\alpha}-\dfrac{sin^2\alpha}{cos^2\alpha}\)bằng
A. \(tan^2\alpha\) ; B . \(cot^2\) α ; C . 0 ; D. 1 .
giải hộ mik vs
Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90 ° . Chọn khẳng định đúng.
A. α + β = 90 °
B. tan α = cot β
C. tan α = cos α
D. tan α = tan β
Đáp án B
Với hai góc α và β mà α + β = 90 °
sin α = cos β ; cos α = sin β
tan α = cot β ; cot α = tan β