Trong khai triển nhị thức Niutơn của a + 2 n + 6 có tất cả 2019 số hạng . Khi đó giá trị n bằng
A. 2012
B. 2013
C. 2018
D. 2019
Những câu hỏi liên quan
Trong khai triển nhị thức Niutơn của a + 2 n + 6 có tất cả 17 số hạng . Khi đó giá trị n bằng
A. 10
B. 11
C. 16
D. 17
Tìm hệ số của số hạng chứa x 3 trong khai triển nhị thức Niutơn ( 2 x - 1 ) 6
A. 160
B. -960
C. 960
D. -160
Chọn D
Xét khai triển nhị thức Niutơn:
(
2
x
-
1
)
6
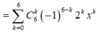
Số hạng chứa x 3 trong khai triển ứng với k = 3.
Vậy hệ số của số hạng chứa
x
3
trong khai triển là: 
.
Đúng 0
Bình luận (0)
Trong khai triển nhị thức Niutơn của
1
+
3
x
9
số hạng thứ 3 theo số mũ tăng dần của x là A.
180
x
2
B.
120
x
2
C.
4
x
2
D.
324
x...
Đọc tiếp
Trong khai triển nhị thức Niutơn của 1 + 3 x 9 số hạng thứ 3 theo số mũ tăng dần của x là
A. 180 x 2
B. 120 x 2
C. 4 x 2
D. 324 x 2
Cho biểu thức P
x
3
-
1
x
10
với x 0. Tìm số hạng không chứa x trong khai triển nhị thức Niutơn P. A. 160 B. 200 C. 210 D. -210
Đọc tiếp
Cho biểu thức P = x 3 - 1 x 10 với x > 0. Tìm số hạng không chứa x trong khai triển nhị thức Niutơn P.
A. 160
B. 200
C. 210
D. -210
Chọn C
Số hạng tổng quát trong khai triển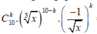 
.
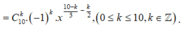Số hạng không chứa x ứng với k thỏa mãn: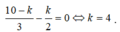 
.
Vậy số hạng không chứa x cần tìm: 
.
Đúng 0
Bình luận (0)
2. Trong khai triển nhị thức ( a +2)^n +6 ( n€N). Có tất cả 17 số hạng . Vậy n bằng?
6. Trong khai triển (2a -1)^6 tổng 3 số hạng đầu là?
7. Trong khai triển ( x - √y )^16 tổng hai số hạng cuối là
2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)
\(\Rightarrow n+6+1=17\Rightarrow n=10\)
6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)
\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)
7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)
\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)
Đúng 0
Bình luận (0)
Gọi
a
2018
là hệ số của số hạng chứa
x
2018
trong khai triển nhị thức Niutơn
x
−
x
n
với
x
≥
0
; n là số nguyên dương thỏa mãn
1
2
!
.2017
!...
Đọc tiếp
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .
Biết rằng khi khai triển nhị thức Niutơn
x
+
1
2
x
4
n
a
0
x
n
+...
Đọc tiếp
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 1 x 4 + a 2 x n - 2 1 x 4 2 + + a 3 x n - 3 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Biết rằng khi khai triển nhị thức Niutơn
x
+
1
2
x
4
n
a
0...
Đọc tiếp
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 . 1 x 4 + a 2 x n - 2 . 1 x 4 2 + a 3 x n - 3 . 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Đáp án C
Yêu cầu bài toán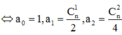 
lập thành cấp số cộng
Khi và chỉ khi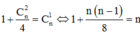 
Do đó, số hạng tổng quát của khai triển là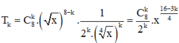 
Số hạng mà lũy thừa của x là số nguyên ứng với 
mà 
Suy ra k = {0;4;8} → Có 3 số hạng lũy thừa của x là số nguyên
Đúng 0
Bình luận (0)
Trong khai triển nhị thức ( a + 2 ) n + 6 có tất cả 17 số hạng. Khi đó giá trị n bằng
A. 12
B. 11
C. 10
D. 17
