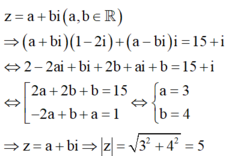Cho số phức z thỏa mãn z 1 + i = 3 - 5 i . Tính môđun của z
A. |z| = 4
B. |z| = 16
C. | z | = 17
D. |z|= 17
Những câu hỏi liên quan
Cho số phức z thỏa mãn (1+z)(1+i)-5+i=0. Số phức w=1+z bằng
A. -1+3i.
B. 1-3i.
C. -2+3i.
D. 2-3i
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn |z| 5 và số phức
w
(
1
+
i
)
z
Tìm |w| A.
10
B.
2
+
5
C. 5 D.
2
5
Đọc tiếp
Cho số phức z thỏa mãn |z| = 5 và số phức w = ( 1 + i ) z Tìm |w|
A. 10
B. 2 + 5
C. 5
D. 2 5
Đáp án A
Phương pháp: Cho z1, z2 là hai số phức bất kì, khi đó | z1.z2 | = |z1|.|z2|
Cách giải: Ta có:
Đúng 0
Bình luận (0)
Cho số phức
z
a
+
b
i
thỏa mãn
z
−
i
≥
3,
z
−
1
≤
5
. Tính
z
1
,
z
2
∈
T
. A. P8 B. P-4 C. P-8 D. P4
Đọc tiếp
Cho số phức z = a + b i thỏa mãn z − i ≥ 3, z − 1 ≤ 5 . Tính z 1 , z 2 ∈ T .
A. P=8
B. P=-4
C. P=-8
D. P=4
Đáp án A
Ta có z ¯ = a − b i thay vào phương trình :
1 + 3 i a + b i + 2 + i a − b i = − 2 + 4 i
⇔ 3 a − 2 b + 4 a − b i = − 2 + 4 i ⇔ a = 2 b = 4 ⇒ a b = 8
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
+
z
)
z
¯
. A. -2 B. 0. C. -...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
z
)
z
¯
.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
Cho số phức z thỏa mãn z - 1 + 2 i =3 . Tìm môđun nhỏ nhất của số phức z-1 +i
A. 4
B. 2 2
C. 2
D. 2
Cho số phức thỏa mãn: za+bi,
(
a
,
b
∈
R
)
thỏa mãn:
z
(
2
+
i
)
z
-
1
+
i
(
2
z
+
3
)
. Tính S a + b
Đọc tiếp
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
Cho số phức z thỏa mãn
z
(
1
-
2
i
)
+
z
¯
i
15
+
i
Tìm môđun của số phức z. A.
z...
Đọc tiếp
Cho số phức z thỏa mãn 
z
(
1
-
2
i
)
+
z
¯
i
=
15
+
i
Tìm môđun của số phức z.
A. z = 5
B. z = 4
C. z = 2 5
D. z = 2 3
Đáp án A
Phương pháp
Gọi 
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
Đúng 0
Bình luận (0)