Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và B A C ^ = 60 0 . Diện tích của hình thoi ABCD là
A. 8 c m 2
B. 8 3 c m 2
C. 16 c m 2
D. 15 c m 2
Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và B A C ^ = 60 0 . Diện tích của hình thoi ABCD là
A. 8 c m 2
B. 8 3 c m 2
C. 16 c m 2
D. 15 c m 2
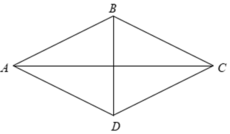
Xét hình thoi ABCD có BACˆ = 600.
Ta có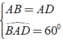 ⇒ Δ ABD đều.
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
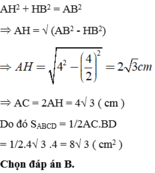
Cho hình thang cân ABCD có AB song song CD,ad = ab = A ,góc ADC = 60° A,B.C,D là trung điểm của AB, BC ,CD, DA
a/ Tính diện tích hình thang ABCD
b/Chứng minh A,B,C,D là hình thoi
Cho hình thoi ABCD có AC = 10 cm, BD = 6cm. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA.
a) Tứ giác EFGH là hình gì? Vì sao?
b) Tính diện tích hình thoi ABCD.
c) Tính diện tích tứ giác EFGH.
a) Ta có EFGH là hình chữ nhật (Tứ giác có 3 góc vuông)
b) S A B C D = 1 2 A C . B D = 30 c m 2
c) SEFGH = EF.FG = 15cm2
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
Cho hình thang cân ABCD có đáy nhỏ AB=6cm,đáy lớn CD=12cm và cạnh bên AD=5cm.Gọi M,N,E,G t/ư là trung điểm của các cạnh AB,BC,CD,DA.
a,CMR : MENG là hình thoi
b,Diện tích hình thoi MENG bằng bao nhiêu cm vuông?
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
a ) Ta có : \(AB=AD=\frac{CD}{2}\) và M là trung điểm của CD (gt)
\(\Leftrightarrow AB=DM\) và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của \(\Delta BDC\) mà MB = MD = MC.
Do đó \(\Delta BDC\) là tam giác vuông tại B hay \(DB\perp BC\)
c) ABMD là hình thoi (cmt) \(\Leftrightarrow\widehat{D}_1=\widehat{D}_2\)
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
\(HB=HD=\frac{1}{2}BD=\frac{1}{2}.4=2\left(cm\right)\)
Xét tam giác vuông AHB, ta có :
\(AH=\sqrt{AB^2-HB^2}\) ( định lí Pitago )
\(=\sqrt{2,5^2-2^2}=1,5\left(cm\right)\)
\(\Rightarrow AM=3\left(cm\right)\)
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
\(\Rightarrow BC=AM=3\left(cm\right)\)
Ta có :
\(S_{BDC}=\frac{1}{2}BD.BC=\frac{1}{2}.4.3=6\left(cm^2\right)\)
M là trung điểm của DC nên
\(S_{BMD}=S_{BMC}=\frac{S_{BCD}}{2}=3\left(cm^2\right)\)
(chung đường cao kẻ từ B và MD = MC)
Mặt khác \(\Delta ABD=\Delta MDB\) ( ABCD là hình thoi )
\(\Leftrightarrow S_{ABD}=S_{BMD}=3\left(cm^2\right)\)
Vậy \(S_{ABCD}=S_{ABD}+S_{BMD}+S_{BMC}=9\left(cm^2\right)\)
Chúc bạn học tốt !!!
Cho hình vuông ABCD có cạnh dài 20cm. Các điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Ta có hình thoi MNPQ. Diện tích của hình thoi là.
MP=(AD+BC)/2=20cm
NQ=(AB+CD)/2=20cm
S MNPQ=1/2*20*20=200cm2
cho hình thoi ABCD có AC= 9cm BD= 6cm ta gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng AB BC CD DA
a) CMR: MNPQ là hình chữ nhật
b) tính tỉ số diện tích của hình chữ nhật MNPQ với diện tích hình thoi ABCD
c) tính diện tích tam giác BMN
tam giácABC : MN là đường trung bình => MN// AC ,tam giác ADC có DP là đường trung bình => QP//AC ==> MN//QP(1) Xét r=tam giác BCD có NP là đường trung binh=> NP//BD=> GÓC MNP=90 ĐỘ(2) từ 1 và 2 => MNPQ là hình chữ nhật b) MNPQ/ABCD=1/2 C) diện tích ABCD=9.6/2=27 , diện tích MNPQ=27/2=13.5 diện tích MNB=3.375
Khoanh vào chữ đặt trước câu trả lời đúng:
Trong hình bên có hình chữ nhật ABCD và hình thoi MNPQ (M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA).
A. Diện tích hình thoi bằng diện tích hình chữ nhật.
B. Diện tích hình thoi lớn hơn 1/2 diện tích hình chữ nhật
C. Diện tích hình thoi bé hơn 1/2 diện tích hình chữ nhật.
D. Diện tích hình thoi bằng 1/2 diện tích hình chữ nhật