Cho hình vẽ bên, biết y A t ^ = 40°, x O y ^ = 140°, O B z ^ = 130° và OA ⊥ OB. Chứng minh At // Bz
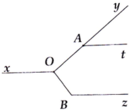
Cho hình vẽ,biết x//y;A1=40*,B1=130*.Qua điểm O vẽ z//x
a)Vì sao z//y
b)Tính AOB
a) Cho hình vẽ, biết Ax //By ,goc A= 30độ,gócAOB= 70 độ. Tính góc B
b) Cho hình vẽ, biết Góc A= 60 độ,góc B= 40 độ. tính số đo x,y
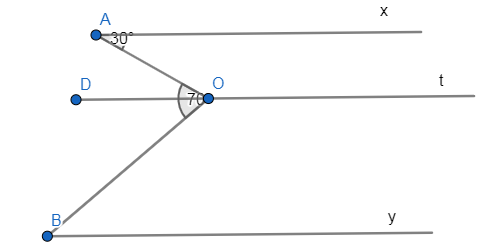
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
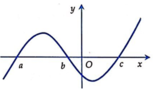
Cho hàm số y=f(x) có đồ thị y=f’(x) như hình vẽ bên. Biết f(a)>0, hỏi đồ thị hàm số y=f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
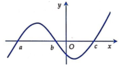
Cho hàm số y = f(x) có đồ thị y = f''(x) như hình vẽ bên. Biết f (a) > 0, hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.
Cho hình vẽ . Biết 2x=3y Tính x , y
Mình ko biết vẽ hình nên mình miêu tả
Vẽ Đường thang xuống , ở phía trên đã/thẳng ( vẫn còn trong đ/thẳng ) vẽ ₫/thẳng AB . Ở phía dưới ₫/thẳng ( vẫn còn trong ₫/thẳng) vẽ ₫/thẳng CD . A=90 độ , C=90 độ , hai góc bên là là x và y ( x ở trên ) ( y ở dưới )
Cho hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ bên dưới. Hàm số y = f 3 − x 2 đồng biến trên khoảng
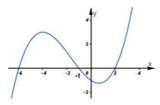
A. (2;3)
B. (-2;-1)
C. (0;1)
D. (-1;0)
Cho hàm số y = f(x) Biết hàm số y = f '(x) có đồ thị như hình vẽ bên dưới. Hàm số y = f 3 − x 2 đồng biến trên khoảng:
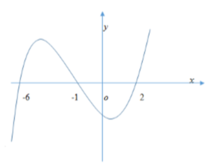
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Đáp án B
Dựa vào đồ thị hàm số ta thấy f ' ( x ) < 0 ⇔ x < − 6 − 1 < x < 2
( f ( 3 − x 2 ) ) ' = ( 3 − x 2 ) ' . f ' ( 3 − x 2 ) = − 2 x . f ' ( 3 − x 2 ) ⇒ ( f ( 3 − x 2 ) ) ' > 0 ⇔ x < − 6 − 1 < x < 0
Cho hàm số y = f(x). Biết hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Hàm số y = 3 - x 2 đồng biến trên khoảng
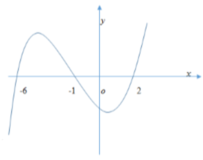
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Cho hàm số y = f(x), biết tại các điểm A, B, C đồ thị của hàm số y = f(x) có tiếp tuyến được thể hiện như hình vẽ bên. Mệnh đề nào dưới đây đúng?
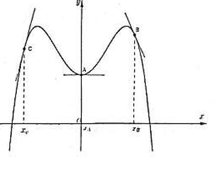
A . f ' ( x C ) < f ' ( x A ) < f ' ( x B ) .
B . f ' ( x A ) < f ' ( x B ) < f ' ( x C ) .
C . f ' ( x A ) < f ' ( x C ) < f ' ( x B ) .
D . f ' ( x B ) < f ' ( x A ) < f ' ( x C ) .
Cho hàm số y=f(x). Biết hàm số y=f'(x) có đồ thị như hình vẽ bên. Hàm số y = f ( 2 x - 3 x 2 ) đồng biển trên khoảng nào dưới đây?