Tổng các nghiệm của phương trình sinx.cosx + |cosx + sinx| = 1 trên (0; 2π) là:
A. π
B. 2π
C. 3π
D. 4π
Những câu hỏi liên quan
Tổng các nghiệm của phương trình
s
i
n
x
.
c
o
s
x
+
s
i
n
x
+
c
o
s
x
1
trên khoảng
0
;
2
π
là A.
2...
Đọc tiếp
Tổng các nghiệm của phương trình s i n x . c o s x + s i n x + c o s x = 1 trên khoảng 0 ; 2 π là
A. 2 π
B. 4 π
C. 3 π
D. π
Cho phương trình sinx.cosx - sinx - cosx + m 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là A.
-
2
≤
m
≤
-
1
2
-
2
B.
-
1
2
-
2
≤
m
≤
1
C.
1
≤...
Đọc tiếp
Cho phương trình sinx.cosx - sinx - cosx + m = 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là
A. - 2 ≤ m ≤ - 1 2 - 2
B. - 1 2 - 2 ≤ m ≤ 1
C. 1 ≤ m ≤ 1 2 + 2
D. 1 2 + 2 ≤ m ≤ 2
Bài 1 tổng tất cả các nghiệm của phương trình sinx/cosx-1=0 trong đoạn [0;4π]
Bài 2 số vị trí biểu diễn tất cả các nghiệm của phương trình cos2x.tan x=0 trên đường tròn lượng giác là
Tính tổng tất cả các nghiệm của phương trình
3
cosx – sinx 1 trên đoạn [0;2π] A.
5
π
3
B.
11
π
6
C.
π
6
D.
3
π...
Đọc tiếp
Tính tổng tất cả các nghiệm của phương trình 3 cosx – sinx = 1 trên đoạn [0;2π]
A. 5 π 3
B. 11 π 6
C. π 6
D. 3 π 2
Giải các phương trình sau:
a/ sinx + cosx = \(2\sqrt{2}\)sinx.cosx
b/ 3sinx - \(\sqrt{3}\)cosx = 0
c/ tanx . sinx +cosx . cosx = sinx + cosx
a) Đặt \(sinx+cosx=t\left(\left|t\right|\le\sqrt{2}\right)\Rightarrow sinx.cosx=\frac{t^2-1}{2}\)
=> pt có dạng: \(t=\sqrt{2}\left(t^2-1\right)\Leftrightarrow\sqrt{2}t^2-t-\sqrt{2}=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=\frac{-\sqrt{2}}{2}\\t=\sqrt{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}sinx+cosx=\frac{-\sqrt{2}}{2}\\sinx+cosx=\sqrt{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}sin\left(x+\frac{\pi}{4}\right)=\frac{-1}{2}\\sin\left(x+\frac{\pi}{4}\right)=1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x+\frac{\pi}{4}=\frac{-\pi}{6}+2k\pi\\x+\frac{\pi}{4}=\frac{7\pi}{6}+2k\pi\\x+\frac{\pi}{4}=\frac{\pi}{2}+2k\pi\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{-5\pi}{12}+2k\pi\\x=\frac{11\pi}{12}+2k\pi\\x=\frac{\pi}{4}+2k\pi\end{cases}}\left(k\inℤ\right)}\)
Cho phương trình:
4
cos
2
x
+
16
sin
x
cos
x
-
7
0
(
1
)
Xét các giá trị: Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1)? A. Chỉ (III) B. (II) và (III) C. Chỉ (II) D. Chỉ (I)
Đọc tiếp
Cho phương trình: 4 cos 2 x + 16 sin x cos x - 7 = 0 ( 1 )
Xét các giá trị:
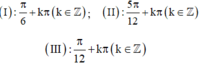
Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1)?
A. Chỉ (III)
B. (II) và (III)
C. Chỉ (II)
D. Chỉ (I)
Đ á p á n B P T đ ã c h o t ư ơ n g đ ư ơ n g : 4 . cos 2 2 x + 8 sin 2 x - 7 = 0 ⇔ 4 . 1 - sin 2 2 x + 8 . sin 2 x - 7 = 0 ⇔ - 4 . sin 2 2 x + 8 . sin 2 x - 3 = 0 ⇔ sin 2 x = 1 2 ⇔ x = π 12 + k π ( k ∈ ℤ ) hoặc x = 5 π 12 + kπ ( k ∈ ℤ )
Đúng 0
Bình luận (0)
Tính tổng hợp tất cả các nghiệm thuộc khoảng
0
;
π
của phương trình:
2
cos
3
x
sin
x
+
cos
x
A.
π
B.
3
π
C.
3
π
2
D.
π
2
Đọc tiếp
Tính tổng hợp tất cả các nghiệm thuộc khoảng 0 ; π của phương trình: 2 cos 3 x = sin x + cos x
A. π
B. 3 π
C. 3 π 2
D. π 2
Số nghiệm của phương trình sinx+cosx=1 trên khoảng (0;π) là
A. 0
B. 1
C. 2
D. 3
Địt mẹ mày, sao đéo thấy đáp án đâu, web đầu buồi
Đúng 0
Bình luận (0)
Cho phương trình: cosx+sinx1+sin2x+cos2x. Nghiệm của phương trình có dạng
x
1
a
π
+
k
π
x
2
±
b...
Đọc tiếp
Cho phương trình: cosx+sinx=1+sin2x+cos2x. Nghiệm của phương trình có dạng x 1 = a π + k π x 2 = ± b π + k 2 π b > 0 . Tính tổng a + b
A. 1 12
B.3
C. 7 π 12
D. π 4
