Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA = AB = 2a, A B C ^ = 60 ° và SA ⊥ (ABCD). Tính khoảng cách từ O đến SB.
A. a 2 2
B. a
C. a 30 4
D. a 3
Cho hình chóp S . A B C D có đáy là hình thoi tâm O cạnh a, A B C ^ = 60 ∘ , S A = S B = S C = 2 a . Tính khoảng cách giữa AB và SC.
A. a 11 8
B. 3 a 11 4
C. a 11 12
D. a 11 12
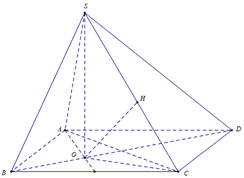
Từ giả thiết suy ra: hình chóp S.ABC là hình chóp đều.
Gọi G là trọng tâm tam giác A B C ⇒ S G ⊥ A B C D
A B / / C D ⇒ A B / / S C D ⇒ d A B ; S C = d A B ; S C D = d B ; S C D = 3 2 d G ; S C D
(Vì B D G D = 3 2 ).
Trong mp (ABCD) vẽ G C ⊥ C D , C D ⊥ S G ⇒ C D ⊥ S G C ⇒ S G C ⊥ S C D
Mà S G C ∩ S C D = S C , vẽ G H ⊥ S C ⇒ d G ; S C D = G H
G B = G C = 2 3 . a 3 2 = a 3 3 .
⇒ S G = S B 2 − B G 2 = 4 a 2 − a 2 3 = a 11 3
Tam giác SHG vuông tại G:
1 G H 2 = 1 S G 2 + 1 G C 2 = 3 11 a 2 + 3 a 2 = 36 11 a 2 ⇒ G H = a 11 6
Vậy d A B ; S C = a 11 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, góc ABC = 60, SA = SB = SC, SD = 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB=a, B A D ^ = 60 ° SO ⊥ (ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp S.ABCD
A. V S . A B C D = 3 a 3 12
B. V S . A B C D = 3 a 3 24
C. V S . A B C D = 3 a 3 8
D. V S . A B C D = 3 a 3 48
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, A B = a , B A D ^ = 60 ° , S O ⊥ A B C D và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp
A. V S . A B C D = 3 a 3 24
B. V S . A B C D = 3 a 3 8
C. V S . A B C D = 3 a 3 12
D. V S . A B C D = 3 a 3 48
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A B C ⏜ = 60 ° , S A ⊥ A B C D , S A = 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 3 a 4
B. 3 a 8 .
C. 5 a 8
D. 5 a 4 .
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Chứng minh: SO ⊥ AB.
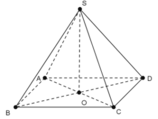
- Hình thoi ABCD có tâm O nên O là trung điểm AC và BD.
+) Tam giác SAC cân tại S( vì SA = SC) có SO là trung tuyến.
⇒ SO cũng là đường cao ⇒ SO ⊥ AC (1)
+) Tam giác SBD cân tại S( vì SB = SD) có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD (2)
- Từ (1), (2) suy ra S) ⊥ (ABCD).
+) Lại có: AB ⊂ mp(ABCD) nên SO ⊥ AB.
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ^ = 60 ° , SA vuông góc với (ABCD) S A = 3 a 2 . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng:
A. 3 a 4
B. 3 a 8
C. 5 a 8
D. 5 a 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, S A ⊥ A B C D . Tìm khẳng định sai?
A. A D ⊥ S C
B. S C ⊥ B D
C. S A ⊥ B D
D. S O ⊥ B D
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, A B C ^ = 60 ° , S A = S B = S C , S D = 2 a . Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V 1 , V 2 trong đó V 1 là thể tích khối đa diện chứa đỉnh S. Tính V 1 V 2
A. 11
B. 7
C. 9
D. 4