Cho tia số sau:
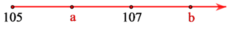
Thay a, b bằng các số
Giá trị của a là ...
Giá trị của b là ...
Những câu hỏi liên quan
Cho các số nguyên a;b;c có giá trị tuyệt đối bằng 3. Khi đó giá trị nhỏ nhất của A=a-b+c là
Cho a và b là các số có một chữ số
a) tìm giá trị lớn nhất của biểu thức a + b và a x b
b) Với giá trị nào của a và b thì a + b bằng a x b
a) Để a + b và a x b lớn nhất và a,b là số có 1 chữ số
=> a = 9 ; b = 9
=> Giá trị lớn nhất của a + b = 9 + 9 = 18
=> Giá trị lớn nhất của a x b = 9 x 9 = 81
b) Khi a = b = 0 hoặc a = b = 2
Đúng 0
Bình luận (0)
a) Đẻ a + b và a x b lớn nhất và a,b là số có 1 chữ số
< = > a = 9 ; b = 9
< = > Gía trị lớn nhất của a + b = 9 + 9 = 18
< = > Gía trị lớn nhất của a x b = 9 x 9 = 81
b) Khi a = b = 0 hoặc a = b = 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a)Cho a là số tự nhiên và a 2525 phần 505. Tìm giá trị lớn nhất của a.Giá trị lớn nhất của a là: ...........................................B) Cho b là sooa tự nhiên và b 2650 phần 53. Tìm giá trị bé nhất của bgiá trị bé nhất của b là: ..........................................Các bạn giải hộ mình nha , mình sẽ cho các bạn điểm hỏi đápMình ko biết cách viết phân số bằng máy tính nên các bạn thông cảm dùm mình nhé
Đọc tiếp
a)Cho a là số tự nhiên và a< 2525 phần 505. Tìm giá trị lớn nhất của a.
Giá trị lớn nhất của a là: ...........................................
B) Cho b là sooa tự nhiên và b > 2650 phần 53. Tìm giá trị bé nhất của b
giá trị bé nhất của b là: ..........................................
Các bạn giải hộ mình nha , mình sẽ cho các bạn điểm hỏi đáp
Mình ko biết cách viết phân số bằng máy tính nên các bạn thông cảm dùm mình nhé
2525/505=5 vậy a lớn nhất =4
2650/53=50 vậy b bé nhất là 51
kết bạn vs mình đi
Đúng 0
Bình luận (0)
Biết rằng tồn tại các số nguyên a, b sao cho hàm số
y
a
x
+
b
x
2
+
1
đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của
a
2
+
2
b...
Đọc tiếp
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
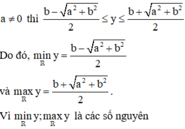
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
Đúng 0
Bình luận (0)
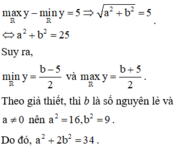
Bài 1 : Cho a và b là các số có 1 chữ số
a, Tìm giá trị lớn nhất của biểu thức a + b và a x b
b, Với giá trị nào của a và b thì a + b bằng a x b
Cho a và b là các số có một chữ số.
a) Tìm giá trị lớn nhất của biểu thức a + b và b + a.
b) Với giá trị nào của a và b thì a + b bằng a x b.
Cho
∫
0
1
x
2
+
x
+
1
x
+
1
d
x
a
+
b
ln
2
với a,b là các số hữu tỷ . Giá trị của a+b bằng A. 0,5 B. 1,5 C. -0,5 D. 2,5
Đọc tiếp
Cho ∫ 0 1 x 2 + x + 1 x + 1 d x = a + b ln 2 với a,b là các số hữu tỷ . Giá trị của a+b bằng
A. 0,5
B. 1,5
C. -0,5
D. 2,5
Cho a,b là các số thực dương thỏa mãn
log
4
a
log
6
b
log
9
(
a
+
b
)
. Giá trị của
a
b
bằng A.
3
2
B.
2
3
C....
Đọc tiếp
Cho a,b là các số thực dương thỏa mãn log 4 a = log 6 b = log 9 ( a + b ) . Giá trị của a b bằng
A. 3 2
B. 2 3
C. 5 + 1 2
D. 5 - 1 2
Cho a, b, c là các số thực dương khác 1 thỏa
log
a
2
b
+
log
b
2
c
log
a
c
b
-
2
log
b
c
b
-...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1 thỏa log a 2 b + log b 2 c = log a c b - 2 log b c b - 3
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = log a b - log b c Giá trị của biểu thức S = 2 m + 3 M bằng
A. S = 1 3
B. S = 2 3
C. S = 2
D. S = 3
Đặt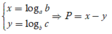 
và giả thiết trở thành
Suy ra 
Phương trình có nghiệm khi 
Chọn D.
Đúng 0
Bình luận (0)