Các câu hỏi tương tự
Giả sử F(x) là một nguyên hàm của hàm số thỏa mãn F(-2) + F(1) 0 và F(-1) + F(2) 0, với a,b là các số hữu tỷ. Giá trị của 3a+6b bằng A. -4 B. 5 C. 0 D. -3
Đọc tiếp
Giả sử F(x) là một nguyên hàm của hàm số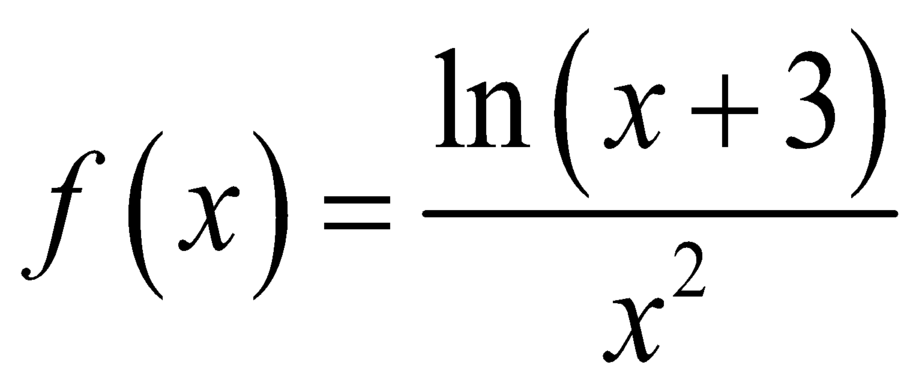 
thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
Giá trị của 3a+6b bằng
A. -4
B. 5
C. 0
D. -3
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
;
f
(
1
)
ln...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2
Tích phân
∫
x
ln
(
x
+
3
)
d
x
a
+
b
ln
2
+
c
ln
5
với a,b,c là các số hữu tỷ. Giá trị của abc bằng A. -30 B. -10 C. -20 D. -15
Đọc tiếp
Tích phân ∫ x ln ( x + 3 ) d x = a + b ln 2 + c ln 5 với a,b,c là các số hữu tỷ. Giá trị của abc bằng
A. -30
B. -10
C. -20
D. -15
Biết
∫
π
4
π
3
cos
2
x
+
sin
x
cos
x
+
1
cos
4
x
+
sin
x...
Đọc tiếp
Biết ∫ π 4 π 3 cos 2 x + sin x cos x + 1 cos 4 x + sin x cos 3 x d x = a + b ln 2 + c ln ( 1 + 3 ) ,
với a, b, c là các số hữu tỉ. Giá trị của abc bằng:
A. 0
B. -2
C. -4
D. -6
Cho
∫
0
1
x
ln
(
2
+
x
2
)
d
x
a
ln
3
+
b
ln
2
+
c
với a,b,c là các số hữu tỷ. Giá trị của a+b+c bằng A. 2 B. 1 C. 1,5 D. 0
Đọc tiếp
Cho ∫ 0 1 x ln ( 2 + x 2 ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỷ. Giá trị của a+b+c bằng
A. 2
B. 1
C. 1,5
D. 0
Cho
∫
1
3
3
+
ln
x
(
x
+
1
)
2
d
x
a
ln
3
+
b
ln
2
+
c
với
a
,
b
,
c...
Đọc tiếp
Cho ∫ 1 3 3 + ln x ( x + 1 ) 2 d x = a ln 3 + b ln 2 + c với a , b , c là các số hữu tỉ. Giá trị của a 2 + b 2 + c 2 bằng
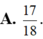
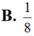
Với giá trị nào của x thì đồ thị hàm số y = 2 / 3 x nằm phía trên đường thẳng y = 1?
A. x > 0 B. x < 0
C. x = 0 D. x < 1
Cho
∫
1
e
(
x
+
2
)
ln
x
d
x
a
e
2
+
b
với a, b là các số hữu tỉ. Giá trị biểu thức a + b bằng A. 10 B.
5
2
C. 2 D.
13
4
Đọc tiếp
Cho ∫ 1 e ( x + 2 ) ln x d x = a e 2 + b với a, b là các số hữu tỉ. Giá trị biểu thức a + b bằng
A. 10
B. 5 2
C. 2
D. 13 4
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x