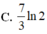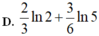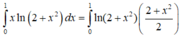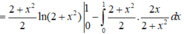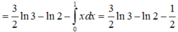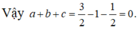Các câu hỏi tương tự
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Biết
∫
1
3
2
+
ln
(
x
+
3
)
(
x
+
1
)
2
d
x
a
ln
2
+
b
ln...
Đọc tiếp
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 d x = a ln 2 + b ln 3 + c ( a , b , c ∈ ℚ ) . Giá trị 3a-b+2c bằng
A. 7
B. 0
C. -2
D. - 11 2
Cho tích phân
∫
0
1
3
x
2
-
2
x
+
ln
(
2
x
+
1
)
d
x
...
Đọc tiếp
Cho tích phân ∫ 0 1 3 x 2 - 2 x + ln ( 2 x + 1 ) d x = b ln a - c với a, b, c là các số hữu tỉ, thì a + b + c bằng
A. 3/2
B. 7/2
C. 2/3
D. -4/3
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số
f
x
1
1
+
sinx
a) F(x) 1 -
cos
x
2
+
π
4...
Đọc tiếp
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Tính giá trị bằng số của biểu thức ln(1/e)
A. 1 B. -1
C. 1/e D. -1/e
Tính giá trị bằng số của biểu thức ln(1/e)
A. 1 B. -1
C. 1/e D. -1/e
Giả sử F(x) là một nguyên hàm của hàm số thỏa mãn F(-2) + F(1) 0 và F(-1) + F(2) 0, với a,b là các số hữu tỷ. Giá trị của 3a+6b bằng A. -4 B. 5 C. 0 D. -3
Đọc tiếp
Giả sử F(x) là một nguyên hàm của hàm số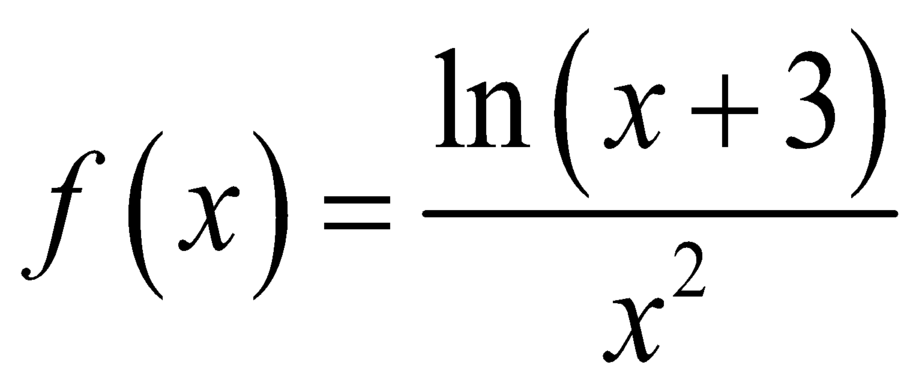 
thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
Giá trị của 3a+6b bằng
A. -4
B. 5
C. 0
D. -3
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
Giả sử F(x) là một nguyên hàm của
f
(
x
)
ln
(
x
+
3
)
x
2
sao cho F(-2)+F(1)0. Giá trị của F(-1)+F(2) bằng B. 0
Đọc tiếp
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
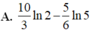
B. 0
