Cho tam giác ABC đều, phép quay tâm A biến B thành C là :
A. Q A ; 120 o
B. Q A ; − 60 o
C. Q A ; 60 o
D. Q A ; 30 o
Cho tam giác đều ABC tâm O. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 120o và phép tịnh tiến theo vectơ biến điểm A thành điểm nào trong các điểm sau?
A. A
B. B
C. O
D. C
Bài 1: Cho hình chữ nhật ABCD có tâm O.Hỏi có bao nhiêu phép quay tâm O, góc quay \(\alpha\), \(0\leq\alpha\leq2\pi\), biến hình chữ nhật thành chính nó?
Bài 2: Cho tam giác đều ABC có tâm O. Phép quay tâm O, góc quay \(\varphi\) biến tam giác đều thành chính nó thì quay \(\varphi\) là góc nào?
Bài 3 Chọn 12 giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu độ?
Bài 4: Cho lục giác đều ABCDEF, O là tâm đối xứng của nó, I là trung điểm AB. Tìm ảnh của tam giác AOF qua phép quay tâm E góc quay \(60^0\)
Bài 5: Trong mặt phẳng Oxy, cho I(2;1) và đường thẳng d: 2x+3y+4=0. Tìm ảnh của d qua \(Q_{(I;45^0)}\)
Bài 6: Trong mặt phẳng Oxy, cho phép tâm O góc quay \(45^0\). Tìm ảnh của đường tròn \((C): (x-1)^2+y^2=4\)
Cho hình vuông ABCD tâm O. Chọn khẳng định đúng:
A. Phép quay tâm A góc quay 90o biến điểm A thành điểm O
B. Phép quay tâm A góc quay 90o biến điểm A thành điểm A
C. Phép quay tâm A góc quay 90o biến điểm A thành điểm B
D. Phép quay tâm A góc quay 90o biến điểm A thành điểm D
Cho hình vuông ABCD. Gọi Q là phép quay tâm A biến B thành D, Q' là phép quay tâm C biến D thành B. Khi đó, hợp thành của hai phép biến hình Q và Q' (tức là thực hiện phép quay Q trước sau đó tiếp tục thực hiện phép quay Q' ) là:
A. Phép quay tâm B góc quay 90 ∘
B. Phép đối xứng tâm B
C. Phép tịnh tiến theo
D. Phép đối xứng trục BC.
Cho hình vuông ABCD. Gọi Q là phép quay tâm A biến B thành D, Q'là phép quay tâm C biến D thành B. Khi đó, hợp thành của hai phép biến hình Q và Q'(tức là thực hiện phép quay Q trước sau đó tiếp tục thực hiện phép quayQ' ) là:
A. Phép quay tâm B góc quay 90 °
B. Phép đối xứng tâm B
C. Phép tịnh tiến theo
D. Phép đối xứng trục BC.
Đáp án B
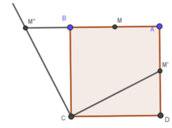
- Chọn một điểm đặc biệt rồi thực hiện liên liếp các phép quay tìm ảnh.
- Đối chiếu các đáp án, đáp án nào có ảnh trùng với ảnh vừa tìm thì nhận.
Cách giải:
Q là phép quay tâm A góc quay 90 ° , Q’là phép quay tâm C góc quay 270 ° .
Gọi M là trung điểm của AB. Phép quay Q biến M thành M’là trung điểm của AD.
Dựng d ⊥ C M ' và d cắt AB tại M”. Khi đó Q’biến M’thành M” .
Khi đó B là trung điểm của MM” nên đó chính là phép đối xứng qua tâm B.
Số phát biểuđúng là:
1.Phép đối xứng qua điểm O là một phép dời hình.
2. Phép đối xứng qua điểm O là phép quay tâm O góc quay 180 °
3. Phép quay Q(O; α ) biến A thành M thì O cách đều A và M
4. Phép quay Q(O; α ) biến A thành M thì O thuộc đường tròn đường kính AM
5. Phép quay Q(O; α ) biến O thành chính nó
6.Phép quay Q(O; α ) biến (O;R) thành (O;2R)
7.Phép quay tâm O góc π 2 và phép quay tâm O góc 5 π 2 là hai phép quay giống nhau
A.4
B.5
C.6
D.7
Đáp án B
Những phát biểuđúng: 1;2;3;5;7
4. Phép quay Q(O;180 ° ) biến A thành M thì O thuộc đường tròn đường kính AM
6. Phép quay Q(O; α ) biến (O;R) thành (O;R)
Cho tam giác ABC có A 2 ; 3 , B 1 ; − 2 , C 6 ; 2 . Phép tịnh tiến T BC → biến tam giác ABC thành tam giác A′B′C′. Tọa độ trọng tâm tam giác A′B′C′ là
A. − 2 ; − 3
B. 2 ; 3
C. 8 ; 5
D. 3 ; 1
cho tam giác ABC có tâm O (các đỉnh ghi theo chiều kim đồng hồ )
a,tìm ảnh của B ,đoạn thẳng BC qua phép quay tâm O góc quay 60 độ
b,tìm ảnh của tam giác OAB qua phép quay tâm O góc quay -120 độ
c, tìm ảnh của tam giác ABC qua phép quay tâm A góc quay tam giác
Cho tam giác ABC có A(2;3),B(1;-2),C(6;2) Phép tịnh tiến T B C ¯ biến tam giác ABC thành
tam giác A’B’C’. Tọa độ trọng tâm tam giác A’B’C’ là
A. (3;1)
B.(-2;-3)
C. (8;5)
D. (2;3)