Cho hình chóp SABC có S A ⊥ A B C . Gọi H, K lần lượt là trực tâm các tam giác SBC vàABC. Mệnh đề nào sai trong các mệnh đề sau
A. B C ⊥ S A H
B. H K ⊥ S B C
C. B C ⊥ S A B
D. SH, AK và BC đồng quy
Bài 17: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, SA = 3a và SA vuông góc với đáy. Gọi H và I lần lượt là trực tâm tam giác ABC và SBC.
a) Chứng minh rằng IH vuông (SBC).
b) Tính thể tích khối tứ diện IHBC theo a
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BH\\BH\perp AC\left(\text{H là trực tâm ABC}\right)\end{matrix}\right.\) \(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
Lại có I là trực tâm SBC \(\Rightarrow BI\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BIH\right)\Rightarrow SC\perp IH\) (3)
Gọi M là giao điểm AH và BC \(\Rightarrow\) M là trung điểm BC (do tam giác ABC đều)
Mà SBC cân tại S (dễ dàng chứng minh SB=SC bằng Pitago) \(\Rightarrow SM\) đồng thời là đường cao trong tam giác SBC hay \(I\in SM\)
\(\Rightarrow IH\in\left(SAM\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AH\perp BC\left(\text{H là trực tâm ABC}\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAM\right)\Rightarrow BC\perp IH\) (4)
(3); (4) \(\Rightarrow IH\perp\left(SBC\right)\)
b.
\(AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow SM=\sqrt{SA^2+AM^2}=\dfrac{a\sqrt{39}}{2}\)
ABC đều nên H là trực tâm đồng thời là trọng tâm \(\Rightarrow\dfrac{MH}{AM}=\dfrac{1}{3}\) \(\Rightarrow MH=\dfrac{AM}{3}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow IM=MH.cos\widehat{AMS}=MH.\dfrac{AM}{SM}=\dfrac{a\sqrt{39}}{78}\)
\(V_{IHBC}=\dfrac{IM}{SM}.\dfrac{MH}{AM}.V_{SABC}=\dfrac{1}{117}.\dfrac{1}{3}.3a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{3}}{468}\)
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Đường thẳng BH vuông góc với đường thẳng:
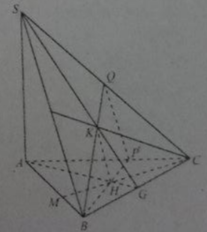
A. AG
B. SC
C. CM
D. SG
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với mặt phẳng:
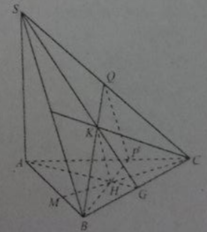
A. (ABC)
B. (SAB)
C. (SAG)
D. (SAC)
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Mặt phẳng (BKH) vuông góc với đường thẳng:
A. SC
B. AC
C. AH
D. AB
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Đường thẳng HK vuông góc với mặt phẳng:
A. (ABC)
B. (BK’H’)
C. (ASG)
D. (SBC)
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với đường thẳng:
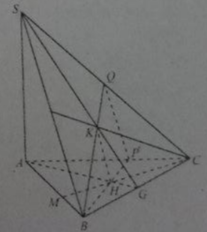
A. SC
B. AC
C. AH
D. AB
Cho hình chóp S.ABC có đường thẳng SA vuông góc với đáy và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm các tam giác ABC và tam giác SBC. Khẳng định nào sau đây đúng?
A. SA, HK, BC đôi một song song
B. AH, BC, SK đồng phẳng
C. SA, HK, BC đôi một chéo nhau
D. AH, SK, BC đồng quy
Tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
a) AH, SK và BC đồng quy.
b) SC vuông góc với mặt phẳng (BHK) và (SAC) ⊥ (BHK)
c) HK vuông góc với mặt phẳng (SBC) và (SBC) ⊥ (BHK)
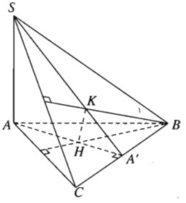
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên AA′ ⊥ BC. Mặt khác theo giả thiết ta có: SA ⊥ (ABC), do đó SA ⊥ BC.
Từ đó ta suy ra BC ⊥ (SAA′) và BC ⊥ SA′. Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên BK ⊥ SC (1)
Mặt khác ta có BH ⊥ AC vì H là trực tâm của tam giác ABC và BH ⊥ SA vì SA ⊥ (ABC).
Do đó BH ⊥ (ABC) nên BH ⊥ SC (2).
Từ (1) và (2) ta suy ra SC ⊥ (BHK). Vì mặt phẳng (SAC) chứa SC mà SC ⊥ (BHK) nên ta có (SAC) ⊥ (BHK).
c) Ta có
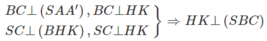
Mặt phẳng (BHK) chứa HK mà HK ⊥ (SBC) nên (BHK) ⊥ (SBC).