Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD là
A. 45⁰.
B. 90⁰.
C. 60⁰.
D. 30⁰.
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng.
A. 60 °
B. 30 °
C. 90 °
D. 45 °
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng.
A. 60 o
B. 30 o
C. 90 o
D. 45 o
Ta có.
C D ⊥ A G C D ⊥ B G ⇒ C D ⊥ A B G ⇒ C D ⊥ A B
Vậy số đo góc giữa hai đường thẳng AB và CD bằng 90 o
Đáp an cần chọn là C
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng
A. 60 o
B. 30 o
C. 90 o
D. 45 o
Đáp án C
Gọi G là trọng tâm tam giác ABC.
Vì tứ diện ABCD đều nên A G ⊥ ( B C D ) .
Ta có C D ⊥ A G C D ⊥ B G
![]()
Vậy số đo góc giữa hai đường thẳng AB và CD bằng 900.
Tứ diện đều ABCD số đo góc giữa hai đường thẳng AB và CD bằng
![]()
![]()
![]()
![]()
Tứ diện đều ABCD số đo góc giữa hai đường thẳng AB và CD bằng
A. 60 °
B. 45 °
C. 30 °
D. 90 °
Đáp án D
Gọi M là trung điểm CD
C D ⊥ B M C D ⊥ A M ⇒ C D ⊥ A B M ⇒ C D ⊥ A B C D ; A B = 90 °
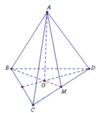
Cho tứ diện ABCD có AB = CD = a, I J = a 3 2 (I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là:
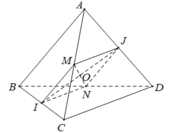
- Gọi M, N lần lượt là trung điểm AC, BC.
+) Tam giác ACD có MJ là đường trung bình của tam giác nên :
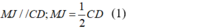
+) Tam giác BCD có NI là đường trung bình của tam giác nên:
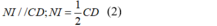
Tương tự, ta có: 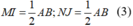
Mà theo giả thiết: AB = CD = a (4)
Từ (1), (2), (3) và (4) suy ra:
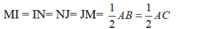
Do đó, tứ giác MJNI là hình thoi ( tính chất hình thoi).
- Gọi O là giao điểm của MN và IJ, ta có:
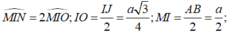
- Xét ΔMIO vuông tại O, ta có:
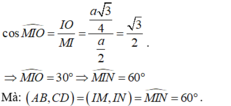
Cho tứ diện ABCD có BC=a, C D = a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
A. a 3 2
B. a 3
C. a
D. a 7 2
Cho tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi là số đo của góc giữa hai đường thẳng AN, CM. Khi đó cosα bằng
A. 2 3
B. 1 3
C. 1
D. 2