Biểu thức Pascal: (a+cos(x))/sqrt(sqr(a)+sqr(x)+1) khi chuyển sang toán học có dạng:
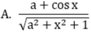
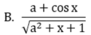

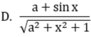
Biểu thức Pascal B: = Sqr(sqrt(x1-x2)+sqrt(y1-y2)) khi chuyển sang toán học có dạng:
![]()
![]()
![]()
![]()
Chuyển biểu thức toán học sang pascal và ngược lại
a) \(\dfrac{1}{2n}\)≤\(\dfrac{3}{5}\)\(\cos\)2π
b)\(\dfrac{\sqrt{x^2+y^{3x}}}{a-\dfrac{a}{b}}z-\dfrac{1}{2}\)
c) Sqrt(a+2/(sqrt(2+a))-(x/a*b)
d) abs(x-2*y)+sqr(x*x)-2*cos(x)
d: \(=\left|x-2y\right|+\left(x\cdot x\right)^2-2\cdot cos\left(x\right)\)
Biểu thức Pascal: b/sqrt(sqr(a)+sqrt(b)) được biểu diễn trong toán học là:
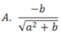
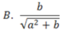
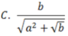
D. Cả A, B, C đều đúng
Biểu thức Pascal: -b/sqrt(sqr(a)+b) được biểu diễn trong toán học là:
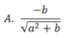
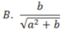
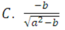
D. Cả A, B, C đều đúng
Chuyển pascal sang toán học :
a) 3* sqr(a)+abs(b)
b) 12/5*sqrt(x)-sqrt(y)
Trong đó : + sqr : bình phương
+ abs : trị tuyệt đối
+ sqrt : \(\sqrt{2}\)
a, 3.a2+ |b|
b, \(\frac{12}{5}\)\(\sqrt{x}\) -\(\sqrt{y}\)
c,
mong các bạn chỉ cho mình với , mai mình có bài kiểm tra 1 tiết .
Biểu thức: sqr(sqrt(x+y)/x-sqr(x-y)/y) viết trong toán học sẽ là biểu thức nào dưới đây?
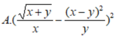
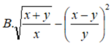
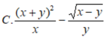
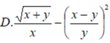
Bài 1 Viết các biểu thức sau sang biểu thức toán học
a) 3*x*x-1/sqr(5)*(x-m)-15=3
b) 8*x-1/sqrt(2+x)+5
(Mong các bạn giúp,mk đang cần gấp, Cảm ơn )
b: \(8x-\dfrac{1}{\sqrt{2+x}}+5\)
a. -> \(3x^2-\dfrac{1}{\sqrt{5}}.\left(x-m\right)-15=3\)
Biểu thức a/(a+1)*(x-1)*(x-1) khi chuyển sang toán học sẽ có dạng:
A. 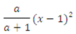
B. 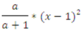
C. 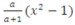
D. 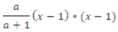
\(1+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{2^2}\)
\(1+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{2^2}\)