Biểu thức: sqr(sqrt(x+y)/x-sqr(x-y)/y) viết trong toán học sẽ là biểu thức nào dưới đây?
Những câu hỏi liên quan
Biểu thức Pascal: (a+cos(x))/sqrt(sqr(a)+sqr(x)+1) khi chuyển sang toán học có dạng:
Đọc tiếp
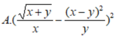
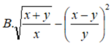
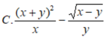
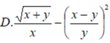
Biểu thức Pascal: (a+cos(x))/sqrt(sqr(a)+sqr(x)+1) khi chuyển sang toán học có dạng:
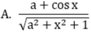
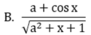
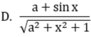
Chuyển biểu thức toán học sang pascal và ngược lại
a) \(\dfrac{1}{2n}\)≤\(\dfrac{3}{5}\)\(\cos\)2π
b)\(\dfrac{\sqrt{x^2+y^{3x}}}{a-\dfrac{a}{b}}z-\dfrac{1}{2}\)
c) Sqrt(a+2/(sqrt(2+a))-(x/a*b)
d) abs(x-2*y)+sqr(x*x)-2*cos(x)
d: \(=\left|x-2y\right|+\left(x\cdot x\right)^2-2\cdot cos\left(x\right)\)
Đúng 1
Bình luận (0)
Biểu thức Pascal: b/sqrt(sqr(a)+sqrt(b)) được biểu diễn trong toán học là:
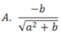
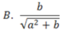
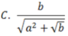
D. Cả A, B, C đều đúng
Biểu thức Pascal: -b/sqrt(sqr(a)+b) được biểu diễn trong toán học là:
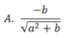
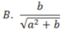
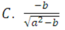
D. Cả A, B, C đều đúng
Bài 1 Viết các biểu thức sau sang biểu thức toán học
a) 3*x*x-1/sqr(5)*(x-m)-15=3
b) 8*x-1/sqrt(2+x)+5
(Mong các bạn giúp,mk đang cần gấp, Cảm ơn )
b: \(8x-\dfrac{1}{\sqrt{2+x}}+5\)
Đúng 1
Bình luận (0)
a. -> \(3x^2-\dfrac{1}{\sqrt{5}}.\left(x-m\right)-15=3\)
Đúng 0
Bình luận (0)
Cho x,y,z>0 và khác nhau đôi một. Chứng minh rằng giá trị của biểu thức P không phụ thuộc vào giá trị của các biến:
P=\(\dfrac{x}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)}+\dfrac{y}{\left(\sqrt{y}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{x}\right)}+\dfrac{z}{\left(\sqrt{z}-\sqrt{x}\right)\left(\sqrt{z}-\sqrt{y}\right)}\)
\(P=\dfrac{x\left(\sqrt{y}-\sqrt{z}\right)-y\left(\sqrt{x}-\sqrt{z}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}+\dfrac{z}{\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{x\sqrt{y}-x\sqrt{z}-y\sqrt{x}+y\sqrt{z}+z\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)-\sqrt{z}\left(x-y\right)+z\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{xy}-\sqrt{z}\left(\sqrt{x}+\sqrt{y}\right)+z\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{\left(\sqrt{xy}-\sqrt{zx}-\sqrt{zy}+z\right)}{\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{y}-\sqrt{z}\right)-\sqrt{z}\left(\sqrt{y}-\sqrt{z}\right)}{\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
\(=\dfrac{\left(\sqrt{y}-\sqrt{z}\right)\left(\sqrt{x}-\sqrt{z}\right)}{\left(\sqrt{x}-\sqrt{z}\right)\left(\sqrt{y}-\sqrt{z}\right)}\)
=1
Đúng 1
Bình luận (0)
13 tháng 12 2022 lúc 22:20
viết biểu thức toán sau đây dưới dạng biểu thức trong pascal x^2+y/y^2+x
\(\dfrac{x^2+y}{y^2+x}\)-> (x*x+y)/(y*y+x)
\(x^2+\dfrac{y}{y^2}+x\) -> x*x+y/y*y+x
x*x và y*y có thể thay thế bằng sqr(x) và sqr(y)
Đúng 3
Bình luận (0)
Viết biểu thức Toán học dưới đây thành biểu thức quan hệ trong Pascal:
M(x;y) ∈ (I(a;b); R)
Biểu thức Pascal B: = Sqr(sqrt(x1-x2)+sqrt(y1-y2)) khi chuyển sang toán học có dạng:
