Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Kẻ AH vuông góc với BC. Gọi D và E lần lượt là điểm đối xứng của H qua AB và AC. Khi đó độ dài đoạn DE bằng: ........................

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH Từ H kẻ HM vuông góc AB HK vuông góc AC (M trên AB,K trên AC
a) chứng minh AH=MK
b)Gọi D và E lần lượt là các điểm đối xứng của H qua AB và A Chứng minh D đối xứng với E qua A
c) chứng minh BD// CE
a: Xét tứ giác AMHK có
góc AMH=góc AKH=góc KAM=90 độ
=>AMHK là hình chữ nhật
=>AH=MK
b: Xét ΔAHD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAHD cân tại A
=>AH=AD và AB là phân giác của góc HAD(1)
Xét ΔHEA có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAHE cân tại A
=>AH=AE và AC là phân giác của góc HAE(2)
Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔAHB và ΔADB có
AH=AD
góc HAB=góc DAB
AB chung
=>ΔAHB=ΔADB
=>góc ADB=90 dộ
=>BD vuông góc DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
góc HAC=góc EAC
AC chung
=>ΔAHC=ΔAEC
=>goc AEC=90 độ
=>CE vuông góc ED(4)
Từ (3), (4) suy ra BD//CE
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có AB = 3cm, AC= 4cm , AH là đường cao . Điểm D ,E lần lượt đối xứng với H qua AB, AC . TÍNH DE?
= 5 cm nhá bạn yêu dấu ơi, còn cách làm thì để mình tìm cách giải thích cho, cái này mình hơi tệ ![]() , thông cảm, mình tìm cách giải thích cho bạn sau
, thông cảm, mình tìm cách giải thích cho bạn sau
Đúng 0
Bình luận (2)
cho tam giác ABC vuông tại A có AB bé hơn AC, gọi E là trung điểm của BC, kẻ EF vuông với AB, ED vuông với AC,O là giao điểm của FD và AE, K là điểm đối xứng với E qua D, kẻ ME vuông với AK tại M, kéo dài BD cắt KC tại I, cho AB=3cm,AC=4cm tính độ dài đoạn KI
Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ HN vuông góc với AC( N thuộc AC ), HM vuông góc với AB(M thuộc AB).a) Cho AB3cm, AC4cm. Tính độ dài BC,MNb) Từ B kẻ đường thẳng vuông góc với BC, cắt AC tại K. Tính độ dài BKc) Gọi D là điểm đối xứng với H qua M, E là điểm đối xứng với H qua N. CMR: Tứ giác AMNE là hình bình hànhd) CMR: BC2 BD2 + CE2 + 2BH.CH
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ HN vuông góc với AC( N thuộc AC ), HM vuông góc với AB(M thuộc AB).
a) Cho AB=3cm, AC=4cm. Tính độ dài BC,MN
b) Từ B kẻ đường thẳng vuông góc với BC, cắt AC tại K. Tính độ dài BK
c) Gọi D là điểm đối xứng với H qua M, E là điểm đối xứng với H qua N. CMR: Tứ giác AMNE là hình bình hành
d) CMR: BC2 = BD2 + CE2 + 2BH.CH
Bạn ơi
Trên đây k đăng hình đc
Bạn vào thống kê hỏi đáp của mk xem đc k nhá!
https://h.vn/hoi-dap/question/937098.html
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH 4cm, CH 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).Tính độ dài đoạn thẳng DE A. DE 5cm B. DE 8cm C. DE 7cm D. DE 6cm
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
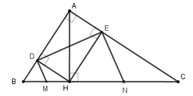
Tính độ dài đoạn thẳng DE
A. DE = 5cm
B. DE = 8cm
C. DE = 7cm
D. DE = 6cm
Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D
Đúng 0
Bình luận (0)
cho tam giác vuông abc vuông tại a(ab<ac), đường cao ah. kẻ hd vuông góc với ab tại d, he vuông góc với ac tại e. chứng minh ah=de. gọi i là điểm đối xứng với a qua e. chứng minh dhie là hình bình hành. cho ab = 15cm ,ac= 20cm,tính bc và ah. gọi f là trung điểm của bh, g là trung điểm của hc. chứng minh df song song với ge
Cho tam giác ABC vuông tại A (AB>AC). Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Trên cạnh AB lấy điểm E sao cho AC=AE.
a) Chứng minh rằng: tam giác ABC = tam giác ADE.
b) Gọi M,N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM=tam giác ABN và AMN vuông cân.
c) Qua E kẻ AH vuông góc với BC tại H. Chứng minh rằng 3 điểm D,E,H thẳng hàng và CE vuông góc với BD
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAMD và ΔANB có
AM=AN
MD=NB
AD=AB
Do đó: ΔAMD=ΔANB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (ABAC). Gọi M, N lần lượt là trung điểm của BC, AC.a) Biết MN 3cm, tính độ dài AB.b) Vẽ điểm D đối xứng với điểm A qua M. CM: tứ giác ABDC là hcn.c) Vẽ điểm K đối xứng với điểm M qua N. CM tứ giác AMCK là hình thoi.d) Vẽ AH vuông góc BC tại H. Gọi E, F lần lượt là trung điểm của HC và BD. CM AE vuông góc EF.d) Qua B vẽ đường thẳng song song EF cắt AH tại T. CM T là trung điểm AH.GIÚP MÌNH CÂU D VỚI C THÔI NHAAA
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC). Gọi M, N lần lượt là trung điểm của BC, AC.
a) Biết MN = 3cm, tính độ dài AB.
b) Vẽ điểm D đối xứng với điểm A qua M. CM: tứ giác ABDC là hcn.
c) Vẽ điểm K đối xứng với điểm M qua N. CM tứ giác AMCK là hình thoi.
d) Vẽ AH vuông góc BC tại H. Gọi E, F lần lượt là trung điểm của HC và BD. CM AE vuông góc EF.
d) Qua B vẽ đường thẳng song song EF cắt AH tại T. CM T là trung điểm AH.
GIÚP MÌNH CÂU D VỚI C THÔI NHAAA

















