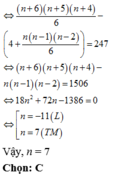trên đường tròn cho n điểm phân biệt. số các tam giác có đỉnh trong số các điểm đã cho là

Những câu hỏi liên quan
Cho hai đường thẳng
d
1
và
d
2
song song với nhau. Trên đường thẳng
d
1
cho 5 điểm phân biệt, trên đường thẳng
d
2
cho 7 điểm phân biệt. Số tam giác có đỉnh là các điểm trong 12 điểm đã cho là: A. 350. B. 210. C. 175. D. 220.
Đọc tiếp
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên đường thẳng d 1 cho 5 điểm phân biệt, trên đường thẳng d 2 cho 7 điểm phân biệt. Số tam giác có đỉnh là các điểm trong 12 điểm đã cho là:
A. 350.
B. 210.
C. 175.
D. 220.
Chọn C
* Số tam giác có 2 đỉnh thuộc
d
1
và 1 đỉnh thuộc
d
2
là: ![]() .
.
* Số tam giác có 1 đỉnh thuộc
d
1
và 2 đỉnh thuộc
d
2
là: ![]() .
.
Vậy có 70 + 105 = 175 tam giác.
Đúng 0
Bình luận (0)
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
![]()
![]()
![]()
![]()
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247 A. 6. B. 8 C. 7. D. 5
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247
A. 6.
B. 8
C. 7.
D. 5
Đáp án C
Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng, tức là không cùng nằm trên một cạnh của tam giác ABC.
Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: C n + 6 3 (cách)
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của tam giác ABC có: C 4 3 + C n 3 (cách)
Số tam giác lập thành là:
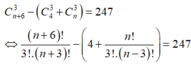
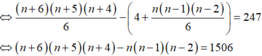
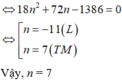
Đúng 0
Bình luận (0)
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247 A. 6 B. 7 C. 5 D. 8
Đọc tiếp
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247
A. 6
B. 7
C. 5
D. 8
Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là:
![]()
Đúng 0
Bình luận (0)
Trên các cạnh a, b, c của một tam giác lần lượt lấy 4, 6, n điểm phân biệt (với \(n>3\) và các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc \(n+10\) điểm đã cho là 736.
Bài 9: a) Cho n tia phân biệt chung gốc tạo thành tất cả 190 góc. Tính n. b) Cho 20 điểm phân biệt cùng nằm trên một đường tròn. Hỏi vẽ được bao nhiêu hình tam giác nhận 3 trong số 20 điểm đã cho là đỉnh?
Cho hai đường thẳng song song
d
1
và
d
2
. Trên đường thẳng
d
1
có 10 điểm phân biệt, trên đường thẳng
d
2
có 20 điểm phân biệt
n
≥
2
. Hỏi có tất cả bao nhiêu tam giác có đỉnh là các điểm đã cho. A. 1000 B. 2000 C. 2400 D. 2800
Đọc tiếp
Cho hai đường thẳng song song d 1 và d 2 . Trên đường thẳng d 1 có 10 điểm phân biệt, trên đường thẳng d 2 có 20 điểm phân biệt n ≥ 2 . Hỏi có tất cả bao nhiêu tam giác có đỉnh là các điểm đã cho.
A. 1000
B. 2000
C. 2400
D. 2800
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n
≥
2). Biết rằng có 1725 tam giác có các đỉnh là ba trong số các điểm thuộc d1 và d2 nói trên. Khi đó n bằng bao nhiêu? A. n 12 B. n 13 C. n 14 D. n 15
Đọc tiếp
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n ≥ 2). Biết rằng có 1725 tam giác có các đỉnh là ba trong số các điểm thuộc d1 và d2 nói trên. Khi đó n bằng bao nhiêu?
A. n = 12
B. n = 13
C. n = 14
D. n = 15
Chọn đáp án D
Một điểm bất kì trên đường thẳng d1 với hai điểm phân biệt trên d2 hoặc cứ một điểm bất kì trên đường thẳng d2 với hai điểm phân biệt trên d1 tạo thành một tam giác.
Vậy tổng sổ tam giác thỏa mãn đề bài là ![]()
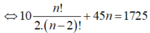
![]()
![]()
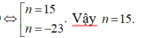
Đúng 0
Bình luận (0)
Cho hai đường thẳng
d
1
và
d
2
song song với nhau. Trên
d
1
có 10 điểm phân biệt, trên
d
2
có n điểm phân biệt (n≥2). Biết rằng có 1725 tam giác có các đỉnh là ba trong số các điểm thuộc
d
1
và
d
2
nói trên. Khi đó n bằng bao nhiê...
Đọc tiếp
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt (n≥2). Biết rằng có 1725 tam giác có các đỉnh là ba trong số các điểm thuộc d 1 và d 2 nói trên. Khi đó n bằng bao nhiêu?
A. 12
B. 13
C. 14
D. 15
Bài 01. Vẽ đường tròn (O) rồi lấy bốn điểm A, B, C, D phân biệt trên đường tròn đó. Vẽ các dây cung có hai đầu là hai trong bốn điểm đã cho. Hỏi trong hình vẽ có:
a) Bao nhiêu dây cung?
b) Bao nhiêu cung tròn?
c) Bao nhiêu tam giác có các đỉnh là ba trong bốn điểm trên?
mk cố nghĩ nhưng mk chịu rồi,mk kém hình lắm.
a) có 2 dây cung
b) có 8 cung tròn
c) có 4 tam giác