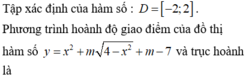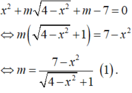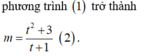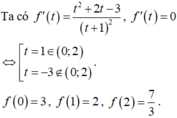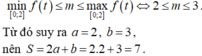tìm tất cả các giá trị của tham số m để hàm số y=x2-2x+m-1 và có trục Ox không có điểm chung

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hai đồ thị hàm số
y
-
x
2
-
2
x
+
3
và
y
x
2
-
m
có điểm chung. A.
m
−
7
2
B.
m
−
7
2
C.
m
−
7
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hai đồ thị hàm số y = - x 2 - 2 x + 3 và y = x 2 - m có điểm chung.
A. m = − 7 2
B. m < − 7 2
C. m > − 7 2
D. m ≥ − 7 2
Phương trình hoành độ giao điểm - x 2 - 2 x + 3 = x 2 - m
⇔ 2 x 2 + 2 x - m - 3 = 0 *
Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm
⇔ ∆ = 1 - 2 - m - 3 ≥ 0 ⇔ m ≥ - 7 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho parabol (P): y x2 – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol (P) không cắt trục Ox. A. m 2. B. m 2. C. D.
Đọc tiếp
Cho parabol (P): y = x2 – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol (P) không cắt trục Ox.
A. m < 2.
B. m > 2.
C. ![]()
D. ![]()
Xét phương trình hoành độ giao điểm:
x2 – 2x + m – 1 = 0 tương đương (x – 1)2 = 2 – m (1)
Để parabol không cắt trục Ox thì phương trình (1) vô nghiệm hay 2 – m < 0 hay m > 2
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số
y
m
x
3
-
x
2
-
2
x
+
8
m
có đồ thị
C
m
. Tìm tất cả các giá trị của tham số m để đồ thị cắt trục hoành tại ba điểm phân biệt. A.
m
∈
-
1
6
;...
Đọc tiếp
Cho hàm số y = m x 3 - x 2 - 2 x + 8 m có đồ thị C m . Tìm tất cả các giá trị của tham số m để đồ thị cắt trục hoành tại ba điểm phân biệt.
A. m ∈ - 1 6 ; 1 2
B. m ∈ - 1 6 ; 1 2
C. m ∈ - 1 6 ; 1 2 \ 0
D. m ∈ - ∞ ; 1 2 \ 0
Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0
Đúng 0
Bình luận (0)
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số
y
x
2
+
m
4
-
x
2
+
m
-
7
có điểm chung với trục hoành là [a;b] (với a;b
∈...
Đọc tiếp
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 2 + m 4 - x 2 + m - 7 có điểm chung với trục hoành là [a;b] (với a;b ∈ ℝ ). Tính giá trị của S = 2a + b.
A. S = 19 3
B. S = 7
C. S = 5
D. S = 23 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
mx
4
+
(
m
-
1
)
x
2
+
2
có đúng 1 điểm cực đại và không có điểm cực tiểu. A. . B. . C. . D. .
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = mx 4 + ( m - 1 ) x 2 + 2 có đúng 1 điểm cực đại và không có điểm cực tiểu.
A. ![]() .
.
B. 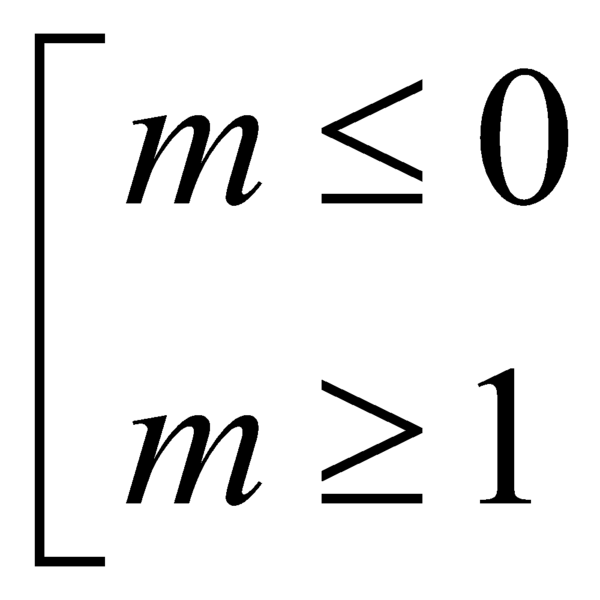 .
.
C. ![]() .
.
D. ![]() .
.
Đáp án C
TH1: ![]() suy ra
suy ra ![]() hàm số có
hàm số có ![]() điểm cực đại
điểm cực đại ![]() nhận m=0.
nhận m=0.
TH2: ![]() .
.
Theo yêu cầu bài toán
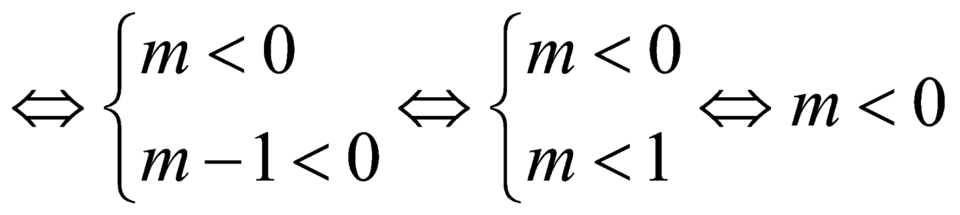 .
.
Vậy ![]() là giá trị cần tìm.
là giá trị cần tìm.
Đúng 0
Bình luận (0)
Cho hàm số
y
m
x
3
-
x
2
-
2
x
+
8
m
có đồ thị
C
m
. Tìm tất cả các giá trị của tham số m để đồ thị
C
m
cắt trục hoành tại ba điểm phân biệt. A.
m
∈
-
1...
Đọc tiếp
Cho hàm số y = m x 3 - x 2 - 2 x + 8 m có đồ thị C m . Tìm tất cả các giá trị của tham số m để đồ thị C m cắt trục hoành tại ba điểm phân biệt.
A. m ∈ - 1 6 ; 1 2
B. m ∈ - 1 6 ; 1 2
C. m ∈ - 1 6 ; 1 2 \ 0
D. m ∈ - ∞ ; 1 2 \ 0
Đáp án C
Phương trình hoành độ giao điểm là:


Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số
y
x
3
+
3
x
2
-
9
x
+
2
m
+
1
và trục Ox có đúng hai điểm chung phân biệt. Tính tổn...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 + 3 x 2 - 9 x + 2 m + 1 và trục Ox có đúng hai điểm chung phân biệt. Tính tổng T của các phần tử thuộc tập S.
A. T = 12.
B. T = 10.
C. I = 8.
D. I = 32.
Tìm tất cả các giá trị tham số m để hai đồ thị hàm số \(y=-x^2-2x+3\) và \(y=x^2-m\) có điểm chung
Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số
y
1
3
x
3
−
x
2
+
m
−
1
x
+
2
có hai điểm cực trị đều nằm bên trái trục tung. A.
1
m
2
B.
m
1
C.
m...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = 1 3 x 3 − x 2 + m − 1 x + 2 có hai điểm cực trị đều nằm bên trái trục tung.
A. 1 < m < 2
B. m > 1
C. m < 2
D. m < 1
Đáp án A
Ta có y ' = x 2 − 2 x + m − 1
Đồ thị hàm số có 2 điểm cực trị đều nằm bên trái trục tung khi y ' = 0 có 2 nghiệm phân biệt đều dương
⇔ Δ ' = 1 − m + 1 > 0 S = 2 > 0 P = m − 1 > 0 ⇔ 2 > m > 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
+
x
2
+
m
cắt trục hoành tại đúng 1 điểm A.
m
−
4
27
hoặc m0 B. m0 C.
m
−
4...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 + x 2 + m cắt trục hoành tại đúng 1 điểm
A. m < − 4 27 hoặc m>0
B. m>0
C. m < − 4 27
D. − 4 27 < m < 0
Đáp án A
PT hoành độ giao điểm:
x 3 + x 2 + m = 0 ⇔ − m = x 3 + x 2 = f x
Xét hàm số: f x = x 3 + x 2 ⇒ f ' x = 3 x 2 + 2 x = 0
⇔ x = 0 ⇒ y = 0 x = − 2 3 ⇒ y = 4 27
Lập BBT hoặc vẽ đồ thị suy ra PT có đúng nghiệm
⇔ − m < 0 − m > 4 27 ⇒ m > 0 m < − 4 27 .
Đúng 0
Bình luận (0)