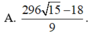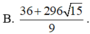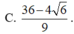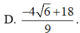(x+3y-5)^5 -6xy+26
tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất
M = (x+3y+5)^2-6xy+26
Tìm giá trị nhỏ nhất , lớn nhất của các biểu thức sau :
a , \(C=6xy-\left(x+3y-5\right)^2-26\)
b, \(D=\left(x+3y-5\right)^2-6xy+26\)
tìm giá trị nhỏ nhất của biểu thức
A = (x + 3y - 5 )2 - 6xy + 26
Tìm Dùm Mình Giá Trị Nhỏ Nhất Của Biểu Thức Sau:
A=(x+3y-5)^2-6xy+26
A = \(x^2+9y^2+25+6xy-30y-10x-6xy+26\)
= \(x^2-10x+25+9y^2-30y+25+1\)
= \(\left(x-5\right)^2+\left(3y-5\right)^2+1\)
Có : \(\left(x-5\right)^2\ge0\forall x;\left(3y-5\right)^2\ge0\forall y\)
\(\Rightarrow A\ge1\)
Vậy GTNN của A là 1 \(\Leftrightarrow\hept{\begin{cases}x-5=0\\3y-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\y=\frac{5}{3}\end{cases}}}\)
Cho 2 số x, y>0 thỏa mãn log 2 x + log x y = log 2 x + 3 y . Giá trị nhỏ nhất của biểu thức sau gần giá trị nào dưới đây nhất P = 2 x . 2 3 y . 2 1 - 3 x - 9 y x 2 + 9 y 2 + 6 x y + 1 .
A. 2
B. 143
C. 2192
D. 3465
Tìm giá trị nhỏ nhất
\(A=x^2-4x\)
\(B=x^2+x+1\)
\(C=\left(x+3y-5\right)^2-6xy+26\)
help me ???
Ta có:\(A=x^2-4x\)
\(A=x^2-4x+4-4\)
\(A=\left(x-2\right)^2-4\le-4\)
Dấu = xảy ra khi x - 2 = 0 ; x = 2
Vậy Min A = - 4 khi x = 2
Ta có:\(B=x^2+x+1\)
\(B=x^2+2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}\)
\(B=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu = xảy ra khi \(x+\frac{1}{2}=0\Rightarrow x=-\frac{1}{2}\)
Vậy MIn B = 3/4 khi x=-1/2
Ta có:\(C=\left(x+3y-5\right)^2-6xy+26\)
\(C=x^2+9y^2+25+6xy-10x-30y-6xy+26\)
\(C=x^2+9y^2-10x-30y+51\)
\(C=x^2-10x+25+9y^2-30y+25+1\)
\(C=\left(x-5\right)^2+\left(3y-5\right)^2+1\ge1\)
Dấu = xảy ra khi \(x-5=0;3y-5=0\Rightarrow x=5;y=\frac{5}{3}\)
Vậy Min C = 1 khi x=5;y=5/3
C= (x+3y-5)2 - 6xy + 26
= x2 + (3y)2 - 25 - 6xy + 26
= x2 - 6xy + (3y)2 + (-25+26)
= x2 - 2.x.3y + (3y)2 + 1
= (x-3y)2 + 1
Vì (x-3y)2 luôn > hoặc = 0
=) (x-3y)2 + 1 luôn > hoặc = 1
vậy GTNN của C là 1
tìm giá trị lớn nhất và giá trị nhỏ nhất
D= 2/3+21/(x+3y)2+5/x+5/+14
a) tìm giá trị nhỏ nhất của biểu thức: A=\(x^2+xy+y^2-3x-3y+2004\)
b) TÌm giá trị nhỏ nhất của biểu thức: A=\(2x^2+9y^2-6xy-6x-12y+2006\)
c) Tìm min của y=\(\frac{x^4+x^2+5}{x^4+2x^2+1}\)
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )