Bày này chỉ có đạt giá trị lớn nhất thôi nhé ! Bạn xem lại đề !

Lời giải :

Gọi \(M\) là trung điểm của \(BC.\) \(\Rightarrow AM\) không đổi.

Kẻ \(KM\perp DE\)

Khi đó tứ giác \(BDEC\) là hình thang. \(\left(BD//KM//EC\right)\)

Xét hình thang \(BDCE\) có : \(M\) là trung điểm của \(BC,\) \(BD//KM//EC\) ( cmt )

\(\Rightarrow K\) là trung điểm của \(DE\)

\(\Rightarrow KM\) là đường trung bình của hình thang \(BDEC\)

\(\Rightarrow BD+EC=2.KM\)

Mặt khác ta có : \(KM\le AM\) nên \(BD+EC\le2AM\) 

Dấu "=" xảy ra \(\Leftrightarrow xy\perp AM\)

Vậy \(BD+CE\) đạt giá trị lớn nhất là \(2AM\) \(\Leftrightarrow xy\perp AM\)

Với mọi vị trí điểm \(M\in BC\), ta luôn có:

\(S_{MAB}+S_{MAC}=S_{ABC}\)

Vì \(\Delta ABM\)có \(BD\perp AM\)

\(\Rightarrow S_{MAB}=\frac{BD.AM}{2}\)
Vì \(\Delta CAM\)có \(CE\perp AM\)

\(\Rightarrow S_{MAC}=\frac{CE.AM}{2}\)

Do đó \(\frac{BD.AM}{2}+\frac{CE.AM}{2}=S_{ABC}\)

\(\Rightarrow\left(BD+CE\right)AM=2S_{ABC}\)

\(\Rightarrow BD+CE=\frac{2S_{ABC}}{AM}\)

Vì \(S_{ABC}\)không đổi \(\Rightarrow2S_{ABC}\)không đổi.

Do đó \(\left(BD+CE\right)_{max}\Leftrightarrow AM_{max}\) 

Giả sử \(AB\le AC\)thì trong 2 đường xiên AM và AC, thì AM là đường xiên ngắn hơn. Do đó  : \(AM\le AC\).

Dấu bằng xảy ra \(\Leftrightarrow M\equiv C\).

\(\Rightarrow\)Đường thẳng xy phải dựng là đường thẳng là đường thẳng chứa cạnh lớn nhất trong 2 cạnh AB hoặc AC thì \(BD+CE\)đạt giá trị lớn nhất.

Vậy...

Gọi D là trung điểm BC. Kẻ MI vuông  với xyy tại I.

Vì BM vuông góc xy

    CN vuông góc xy

    DI vuông góc xy

=> BM // CN // DI

Vì BM // CN

=> BMNC là hình thang

mà D là trung điểm BC, DI // BM // CN

=> I là trung điểm MN 

mà D là trung điểm BC

=> DI là đường trung bình của hình thang BMNC.

=> DI = \(\frac{BM+CN}{2}\)

=> BM + CN = 2DI

Có DI < DA ( quan hệ giữa đường vuông góc và đường xiên.

Để BM + CN lớn nhất

thì DI lớn nhất

=> DI trùng AD

=> DA vuông góc với xy

Vậy,  nếu xy vuông góc với đường trung tuyến AD của tam giác ABC thì BM + CN lớn nhất.

Sao lại thế được. Xin lỗi nhưng cách giải của bạn hơi mâu thuẫn...

bạn có làm được trường hợp xy cắt BC không? Cảm ơn

Vì △ABC vuông cân tại A (gt) => AB = AC và ∠ABC = ∠ACB = 45^o 

Để xy không cắt BC <=> xy // BC <=> DE // BC => ∠ABC = ∠BAD = 45^o  , ∠ACB = ∠CAE = 45^o 

Lại có: +) DE // BC (cmt) mà BD ⊥ DE (gt) 

=> BC ⊥ BD (từ vuông góc đến song song) 

+) DE // BC (cmt) mà CE ⊥ DE (gt) 

=> BC ⊥ CE (từ vuông góc đến song song) 

Xét △BAD vuông tại D có: ∠BAD + ∠ABD = 90^o (tổng 2 góc nhọn trong △ vuông) 

=> 45^o + ∠ABD = 90^o  

=> ∠ABD = 45^o mà ∠BAD =45^o  

=> ∠ABD = ∠BAD 

=> △ABD vuông cân tại D 

=> BD = DA 

Xét △CAE vuông tại E có: ∠CAE + ∠ACE = 90^o (tổng 2 góc nhọn trong △ vuông) 

=>45^o + ∠ACE = 90^o  

=> ∠ACE = 45^o mà ∠CAE = 45^o  

=> ∠CAE = ∠ACE 

=> △CAE vuông cân tại E 

=> EA = EC 

Xét △BCD vuông tại B và △EDC vuông tại E 

Có: ∠BDC = ∠DCE (BC // DE)

       DC là cạnh chung 

=> △BCD = △EDC (ch-gn) 

=> BC = DE (2 cạnh tương ứng) 

=> BC = DA + AE 

=> BD + EC = BC (đpcm)

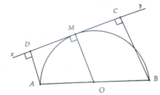
Ta có ABCD là hình thang vuông tại C và D

Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)

=> AD+BC=2OM=2R.  Chú ý rằng CD ≤ AB (hình chiếu đường xiên)

=>  S A B C D = 1 2 A D + B C . C D

= R.CD ≤ R.AB = 2 R 2

Do đó S A B C D  lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB

Hà Nguyễn

BD+ CE +BC ??
Đề đúng có pk là : BD + CE = BC ??

J